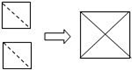
把两个相同的正方形剪一剪,拼一拼(这里的剪拼应该是无重叠且无缝隙的),拼成一个大正方形,除了如图所示的方法外,请你再用另一种方法剪拼一下,画出示意图
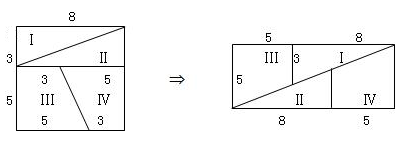
小王把一个边长为8的正方形剪成4块,如下图画成了一个矩形,示意他的拼图方法,你认为这样的拼图方法正确吗?用一句话说明理由
先化简,再求值: ,其中 .
如图,已知抛物线 与 轴交于点 ,点 (点 在点 的左边),与 轴交于点 ,点 为抛物线的顶点,连接 .直线 经过点 ,且与 轴交于点 .
(1)求抛物线的解析式;
(2)点 是抛物线上的一点,当 是以 为腰的等腰三角形时,求点 的坐标;
(3)点 为线段 上的一点,点 为线段 上的一点,连接 ,并延长 与线段 交于点 (点 在第一象限),当 且 时,求出点 的坐标.

如图所示,四边形 为正方形,在 中, , , 的延长线与 的延长线交于点 ,点 、 、 在同一条直线上.
(1)求证: ;
(2)当 时,求 的值;
(3)当 , 时,求 的值.

如图,在 中, ,以 为直径的 与 相交于点 , ,垂足为 .
(1)求证: 是 的切线;
(2)若弦 垂直于 ,垂足为 , , ,求 的半径;
(3)在(2)的条件下,当 时,求线段 的长.

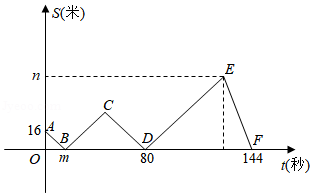
小刚和小亮两人沿着直线跑道都从甲地出发,沿着同一方向到达乙地,甲乙两地之间的距离是720米,先到乙地的人原地休息.已知小刚先从甲地出发4秒后,小亮从甲地出发,两人均保持匀速前行第一次相遇后,保持原速跑一段时间,小刚突然加速,速度比原来增加了2米 秒,并保持这一速度跑到乙地(小刚加速过程忽略不计).小刚与小亮两人的距离 (米 与小亮出发时间 (秒 之间的函数图象,如图所示.根据所给信息解决以下问题.
(1) , ;
(2)求 和 所在直线的解析式;
(3)直接写出 为何值时,两人相距30米.