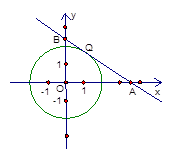
小刚和小亮两人沿着直线跑道都从甲地出发,沿着同一方向到达乙地,甲乙两地之间的距离是720米,先到乙地的人原地休息.已知小刚先从甲地出发4秒后,小亮从甲地出发,两人均保持匀速前行第一次相遇后,保持原速跑一段时间,小刚突然加速,速度比原来增加了2米 秒,并保持这一速度跑到乙地(小刚加速过程忽略不计).小刚与小亮两人的距离 (米 与小亮出发时间 (秒 之间的函数图象,如图所示.根据所给信息解决以下问题.
(1) , ;
(2)求 和 所在直线的解析式;
(3)直接写出 为何值时,两人相距30米.
如图,ABCD是边长为1的正方形,其中 、
、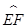 、
、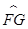 的圆心依次是点A、B、C.
的圆心依次是点A、B、C.
(1)求点D沿三条圆弧运动到G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.
张彬 和王华两位同学为得到一张观看足球比赛的入场券,各自设计了一种方案:
张彬:如图,设计了一个可以自由转动的转盘,随意转动转盘,当指针指向阴影区域时,张彬得到了入场券;否则,王华得到入场券;
王华:将三个完全相同的小球分别标上数字1、2、3后,放入一个不透明的袋子中.从中随机取出一个小球,然后放回袋子;混合均匀后,再随机取出一个小球.若两次取出的小球上的数字之和为偶数,王华得到入场券;否则,张彬得到入场券.
请你运用所学的概率知识,分析张彬和王华 的设计方案对双方是否公平.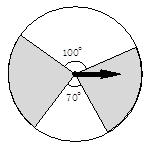
下图是2006年某省各类学校在校生数情况制作的扇形统计图和不完整的条形统计图.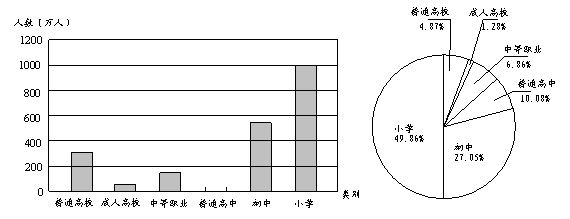
已知2006年该省普通高校在校生为97.41万人,请根据统计图中提供的信息解答下列问题:
(1)2006年该省各类学校在校生总人数约多少万人?(精确到1万)
(2)补全条形统计图;
(3)请你写出一条合理化建议.
如图,点E、F、G分别 是□ABCD的边AB、BC、CD、DA的中点.求证:ΔBEF≌ΔDGH.
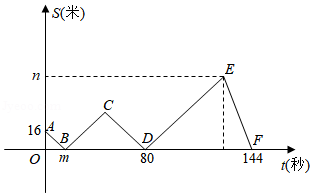
如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与 轴相交于点A,与
轴相交于点A,与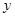 轴相交于点B。
轴相交于点B。
(1)点P在运动时,线段AB的长度页在发生变化,请写出线段AB长度的最小值,并说明理由;
(2)在⊙O上是否存在一点Q,使得以Q、O、A、P为顶点的四边形时平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由。