如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。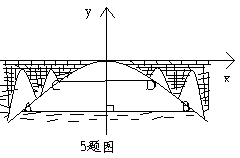
(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
2010年度东风公司神鹰汽车改装厂开发出A型农用车,其成本价为每辆2万元,出厂价为每辆2.4万元,年销售价为10000辆,2011年为了支援西部大开发的生态农业建设,该厂抓住机遇,发展企业,全面提高A型农用车的科技含量,每辆农用车的成本价增长率为x,出厂价增长率为0.75x,预测年销售增长率为0.6x.(年利润=(出厂价-成本价)×年销售量)
(1)求2011年度该厂销售A型农用车的年利润y(万元)与x之间的函数关系。
(2)该厂要是2001年度销售A型农用车的年利润达到4028万元,该年度A型农用车的年销售量应该是多少辆?
已知二次函数y=x2+bx+c的图像与x轴的两个交点的横坐标分别为x1、x2,一元二次方程x2+b2x+20=0的两实根为x3、x4,且x2-x3=x1-x4=3,求二次函数的解析式,并写出顶点坐标。
某商场将进价为30元的书包以40元售出,平均每月能售出600个,调查表明:这种书包的售价每上涨1元,其销售量就减少10个。
(1)请写出每月售出书包的利润y元与每个书包涨价x元间的函数关系式;
(2)设每月的利润为10000的利润是否为该月最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时书包的售价应定为多少元。
(3)请分析并回答售价在什么范围内商家就可获得利润。
二次函数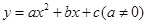 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题: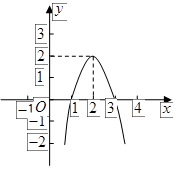
(1)写出方程 的两个根;
的两个根;
(2)写出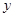 随
随 的增大而减小的自变量
的增大而减小的自变量 的取值范围;
的取值范围;