在平面直角坐标系中,抛物线 与 轴相交于点 (点 在点 的左侧),与 轴相交于点 ,连接 .
(1)求点 ,点 的坐标;
(2)如图1,点 在线段 上(点 不与点 重合),点 在 轴负半轴上, ,连接 ,设 的面积为 , 的面积为 , ,当 取最大值时,求 的值;
(3)如图2,抛物线的顶点为 ,连接 ,点 在第一象限的抛物线上, 与 相交于点 ,是否存在点 ,使 ,若存在,请求出点P的坐标;若不存在,请说明理由.

在平面直角坐标系中,如图所示,△ABC是边长为2的等边三角形,将△ABC绕着点B按顺时针方向旋转得到△EDB,使得点E落在 轴的正半轴上,连结CE、AD、
轴的正半轴上,连结CE、AD、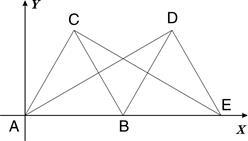
(1)求证:AD=CE;
(2)求AD的长;
(3)求过C、E两点的直线的解析式.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3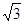 ,AE=3,求AF的长.
,AE=3,求AF的长.
小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件:如果一次性购买不超过10件,单价为80元;如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元.按此优惠条件,小丽一次性购买这种服装付了1200元.请问她购买了多少件这种服装?
气象台发布的卫星云图显示,代号为W的台风在某海岛(设为点O)的南偏东450方向的B点生成,测得 。台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处。因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西600方向继续移动,以O为原点建立如图所示的直角坐标系。
。台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处。因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西600方向继续移动,以O为原点建立如图所示的直角坐标系。
(1)台风中心生成点B的坐标为(),台风中心转折点C的坐标为();(结果保留根号)
(2)已知距台风中心20km的范围内均会受到台风的侵袭.如果某城市(设为点A)位于点O的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
从全校1200名学生中随机选取一部分学生进行调查,调查情况:A:上网时间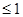 小时;B:1小时<上网时间
小时;B:1小时<上网时间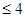 小时;C:4小时<上网时间
小时;C:4小时<上网时间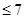 小时;D:上网时间>7小时.统计结果制成了如
小时;D:上网时间>7小时.统计结果制成了如
图统计图: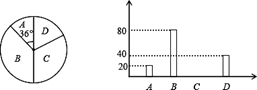
(1)参加调查的学生有 人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数.