下表是我国一个工业城市每年中度以上污染的天数,由于以前只注重经济发展,没有过多的考虑工业发展对环境的影响,近几年来,该市加大了对污染企业的治理整顿,环境不断得到改善。
| 年份(x) |
2005年 |
2006年 |
2007年 |
2008年 |
2009年 |
| 中度以上污染的天数(y) |
90 |
74 |
62 |
54 |
45 |
(1)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(2)按照环境改善的趋势,估计2012年中度以上污染的天数。
(3)在以上5年中任取2年,至少有1年中度以上污染的天数小于60天的概率有多大。
(可用公式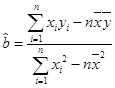 ,
,  )
)
(理)(本小题满分14分)
已知数列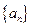 满足
满足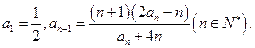
(Ⅰ)求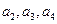 ;(Ⅱ)已知存在实数
;(Ⅱ)已知存在实数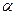 ,使
,使 为公差为
为公差为 的等差数列,求
的等差数列,求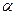 的值;(Ⅲ)记
的值;(Ⅲ)记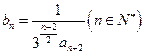 ,数列
,数列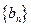 的前
的前 项和为
项和为 ,求证:
,求证: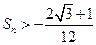 .
.
(本小题共13分)已知动圆过定点 ,且与直线
,且与直线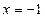 相切.(1)求动圆的圆心轨迹
相切.(1)求动圆的圆心轨迹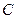 的方程;(2) 是否存在直线
的方程;(2) 是否存在直线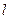 ,使
,使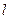 过点(0,1),并与轨迹
过点(0,1),并与轨迹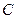 交于
交于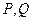 两点,且满足
两点,且满足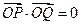 ?若存在,求出直线
?若存在,求出直线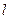 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.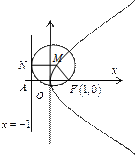
已知曲线 ,从
,从 上的点
上的点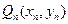 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,再从点
,再从点 作
作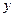 轴的垂线,交
轴的垂线,交 于点
于点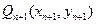 ,设
,设
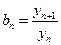
(1)求数列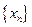 的通项公式;
的通项公式;
(2)记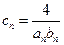 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与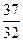 的大小
的大小 ;
;
(3)记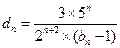 ,数列
,数列 的前
的前 项和为
项和为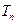 ,试证明:
,试证明:
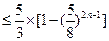
已知椭圆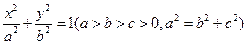 的左、右焦点分别为
的左、右焦点分别为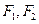 ,若以
,若以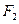 为圆心,
为圆心,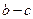 为半径作圆
为半径作圆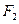 ,过椭圆上一点
,过椭圆上一点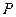 作此圆的切线,切点为
作此圆的切线,切点为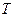 ,且
,且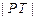 的最小值不小于为
的最小值不小于为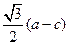 .
.
(1)求椭圆的离心率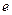 的取值范围;
的取值范围;
(2)设椭圆的短半轴长为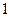 ,圆
,圆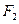 与
与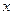 轴的右交点为
轴的右交点为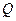 ,过点
,过点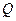 作斜率为
作斜率为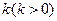 的直线
的直线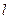 与椭圆相交于
与椭圆相交于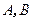 两点,若
两点,若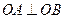 ,求直线
,求直线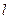 被圆
被圆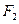 截得的弦长
截得的弦长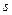 的最大值.
的最大值.
已知函数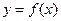 的反函数为
的反函数为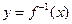 ,定义:若对给定的实数
,定义:若对给定的实数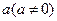 ,函数
,函数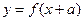 与
与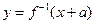 互为反函数,则称
互为反函数,则称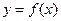 满足“
满足“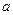 和性质”.
和性质”.
(1)判断函数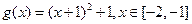 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2)若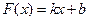 ,其中
,其中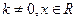 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得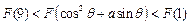 对任意的
对任意的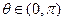 恒成立?若存在,求出
恒成立?若存在,求出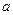 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.