(理)(本小题满分14分)
已知数列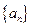 满足
满足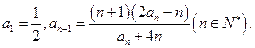
(Ⅰ)求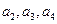 ;(Ⅱ)已知存在实数
;(Ⅱ)已知存在实数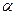 ,使
,使 为公差为
为公差为 的等差数列,求
的等差数列,求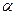 的值;(Ⅲ)记
的值;(Ⅲ)记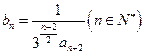 ,数列
,数列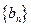 的前
的前 项和为
项和为 ,求证:
,求证: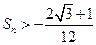 .
.
(本小题满分14分)设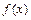 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,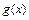 的图象与
的图象与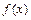 的图象关于直线
的图象关于直线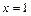 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,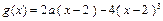 222233.
222233.
(1)求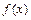 的解析式;
的解析式;
(2)若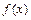 在
在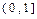 上为增函数,求
上为增函数,求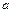 的取值范围;
的取值范围;
(3)是否存在正整数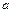 ,使
,使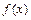 的图象的最高点落在直线
的图象的最高点落在直线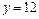 上?若存在,求出
上?若存在,求出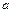 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分13分)设函数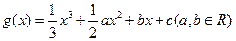 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为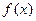 .
.
(1)若方程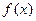 =0有两个实根分别为-2和4,求
=0有两个实根分别为-2和4,求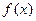 的表达式;
的表达式;
(2)若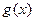 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求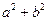 的最小值.
的最小值.
定义在R上的单调函数f(x)满足f(3)=log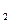 3且对任意x,y∈R都有f(x+y)=f(x)+f(y).
3且对任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求证f(x)为奇函数;
(2)若f(k·3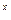 )+f(3
)+f(3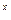 -9
-9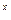 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
已知函数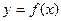 是
是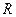 上的奇函数,当
上的奇函数,当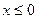 时,
时, ,
,
(1)判断并证明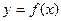 在
在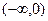 上的单调性;
上的单调性;
(2)求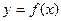 的值域;
的值域;
(3)求不等式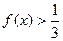 的解集。
的解集。
已知函数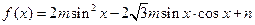 的定义域为
的定义域为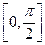 ,值域为
,值域为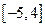 .试求函数
.试求函数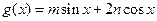 (
(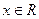 )的最小正周期和最值
)的最小正周期和最值