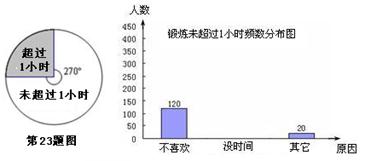
某中学为了了解学生体育活动情况，随即调查了720名初二学生，调查内容是：“每天锻炼是否超过1小时及未超过1小时的原因”，利用所得的数据制成了扇形统计图和频数分布直方图.根据图示，解答下列问题：若在被调查的学生中随机选出一名学生测试其体育成绩，选出的是“每天锻炼超过1小时”的学生的概率是多少？
“没时间”锻炼的人数是多少？并补全频数分布直方图；
2012年宁波市区初二学生约为2万人，按此调查，可以估计2012年宁波市区初二学生中每天锻炼未超过1小时的学生约有多少万人？
请根据以上结论谈谈你的看法.
的值．
与(6－27)2互为相反数，求
的立方根．