(本小题满分12分)已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明: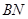 ⊥平面
⊥平面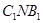 ;
;
(Ⅱ)求平面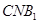 与平面
与平面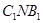 所成角的余弦值;
所成角的余弦值;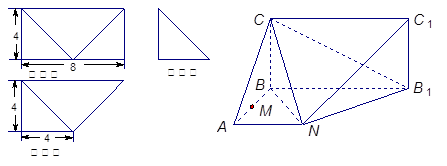
(本小题满分12分)
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(I)假设n=2,求第一大块地都种植品种甲的概率;
(II)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
| 品种甲 |
403 |
397 |
390 |
404 |
388 |
400 |
412 |
406 |
| 品种乙 |
419 |
403 |
412 |
418 |
408 |
423 |
400 |
413 |
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据 的的样本方差
的的样本方差 ,其中
,其中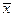 为样本平均数.
为样本平均数.
(本小题满分12分)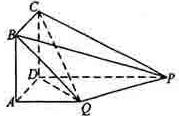
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= PD.
PD.
(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q—ABCD的的体积与棱锥P—DCQ的体积的比值.
(本小题满分12分)
△ABC的三个内角A,B,C所对的边分别为a,b,c,asinAsinB+bcos2A=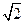 a.
a.
(I)求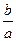 ;
;
(II)若c2=b2+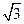 a2,求B.
a2,求B.
(本小题满分12分)
设函数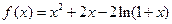 .
.
(1)求函数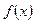 的单调区间;
的单调区间;
(2)当 时,是否存在整数
时,是否存在整数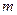 ,使不等式
,使不等式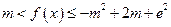 恒成立?若
恒成立?若
存在,求整数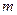 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3)关于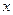 的方程
的方程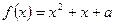 在
在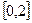 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数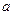 的取值范围。
的取值范围。
.(本小题满分12分)
已知数列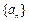 满足:
满足: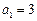 ,
,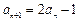 ,
,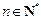 .计算得
.计算得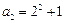 ,
,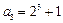 .
.
(1)猜想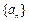 的通项公式
的通项公式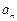 ,并用数学归纳法加以证明;
,并用数学归纳法加以证明;
(2)用反证法证明数列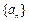 中不存在成等差数列的三项.
中不存在成等差数列的三项.