设计一个算法,求1+2+4+…+249的值,并画出程序框图.
(本小题满分14分)
已知函数 的反函数为
的反函数为 ,数列
,数列 和
和 满足:
满足: ,
, ;函数
;函数 的图象在点
的图象在点 处的切线在y轴上的截距为
处的切线在y轴上的截距为 .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若数列 的项仅
的项仅 最小,求
最小,求 的取值范围;
的取值范围;
(3)令函数 ,
, ,数列
,数列 满足:
满足: ,
, ,且
,且 ,其中
,其中 .证明:
.证明: .
.
(本大题满分13分)
在△ABC中,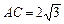 ,点B是椭圆
,点B是椭圆 的上顶点,l是双曲线
的上顶点,l是双曲线 位于x轴下方的准线,当AC在直线l上运动时.
位于x轴下方的准线,当AC在直线l上运动时.
(1)求△ABC外接圆的圆心 的轨迹E的方程;
的轨迹E的方程;
(2)过定点F(0,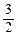 )作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.
)作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.
(本小题满分12分)
已知函数 的定义域为R, 对任意实数
的定义域为R, 对任意实数 都有
都有 ,
,
且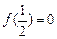 , 当
, 当 时,
时,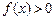 .
.
(1) 求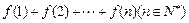 ;
;
(2) 判断函数 的单调性并证明.
的单调性并证明.