(1)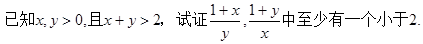
(2) 已知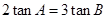 ,求证:
,求证: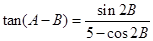 .
.
已知数列{an}满足a1=4,an=4- (n≥2),令bn=
(n≥2),令bn= .
.
(1)求证数列{bn}是等差数列;
(2)求数列{an}的通项公式.
设函数 ,数列
,数列 的通项
的通项 满足
满足 .
.
(1)求数列 的通项公式;(2)判定数列{a n }的单调性.
的通项公式;(2)判定数列{a n }的单调性.
数列{an}是首项为23,公差为整数的等差数列,且第六项为正,第七项为负.
(1)求数列的公差;
(2)求前n项和Sn的最大值;
(3)当Sn>0时,求n的最大值.
在数列{an}中,a1=2,a17=66,通项公式是项数n的一次函数.
(1)求数列{an}的通项公式;
(2)88是否是数列{an}中的项.
已知关于x的方程x2-3x+a=0和x2-3x+b=0(a≠b)的四个根组成首项为 的等差数列,求a+b的值.
的等差数列,求a+b的值.