已知数列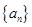 中,
中,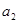 =
= (
(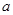 为常数);
为常数);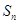 是
是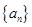 的前
的前 项和,且
项和,且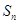 是
是 与
与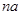 的等差中项。
的等差中项。
(1)求 ;
;
(2)猜想 的表达式,并用数学归纳法加以证明;
的表达式,并用数学归纳法加以证明;
(3)求证以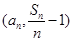 为坐标的点
为坐标的点 都落在同一直线上。
都落在同一直线上。
已知A(5,1),B(7,-3),C(2,-8),求△ABC的外接圆的方程。
在△ABC中,边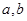 的长是方程
的长是方程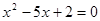 的两根,
的两根,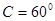 求边c的长。
求边c的长。
(本题共12分)
已知函数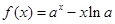 ,其中
,其中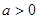 且
且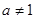 。
。
(Ⅰ)讨论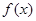 的单调性;
的单调性;
(Ⅱ)求函数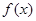 在〔
在〔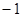 ,
,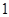 〕上的最小值和最大值。
〕上的最小值和最大值。
(本题共12分)
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量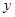 (升)与
(升)与
行驶速度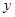 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: 。已知甲、乙
。已知甲、乙
两地相距100千米。
(I)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(本题共10分)
将两块三角板按图甲方式拼好,其中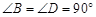 ,
,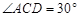 ,
,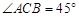 ,
,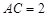 ,现将三角板
,现将三角板 沿
沿 折起,使
折起,使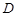 在平面
在平面 上的射影恰好在
上的射影恰好在 上,如图乙.
上,如图乙.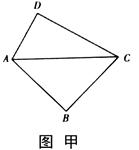
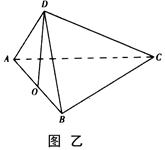
(Ⅰ)求证: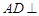 平面
平面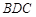 ;
;
(Ⅱ)求二面角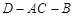 的余弦值;
的余弦值;