如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC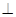 BD,垂足为H,PH是
BD,垂足为H,PH是
四棱锥的高 ,E为AD中点;(Ⅰ)证明:PE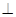 BC;
BC;
(Ⅱ)若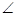 APB=
APB=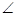 ADB=60°,求直线PA与平面PEH所成角的正弦值。
ADB=60°,求直线PA与平面PEH所成角的正弦值。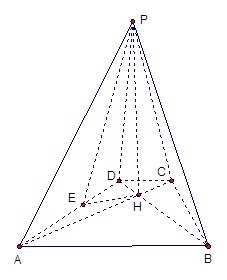
如图,用长为12米的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径为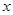 米.
米.
(Ⅰ)求此框架围成的面积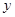 与
与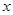 的函数式
的函数式 ,并写出它的定义域;
,并写出它的定义域;
(Ⅱ)求半圆的半径是多长时,窗户透光的面积最大?
求下列函数的定义域:
(Ⅰ) ;
;
(Ⅱ)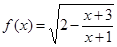 .
.
已知全集为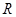 ,集合
,集合 ,集合
,集合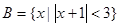 .
.
求:(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
(本小题满分12分)已知椭圆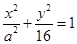 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过 的椭圆的右焦点
的椭圆的右焦点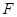 任作一条斜率为
任作一条斜率为 (
( )的直线交椭圆于A,B两点,问在
)的直线交椭圆于A,B两点,问在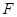 右侧是否存在一点D
右侧是否存在一点D ,连AD、BD分别交直线
,连AD、BD分别交直线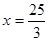 于M,N两点,且以MN为直径的圆恰好过
于M,N两点,且以MN为直径的圆恰好过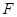 ,若存在,求
,若存在,求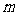 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)数列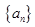 中,已知
中,已知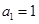 ,
, 时,
时, .数列
.数列 满足:
满足: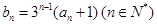 .
.
(Ⅰ)证明: 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为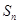 ,是否存在正整数
,是否存在正整数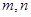 ,使得
,使得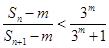 成立?若存在,求出所有符合条件的有序实数对
成立?若存在,求出所有符合条件的有序实数对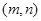 ;若不存在,说明理由.
;若不存在,说明理由.