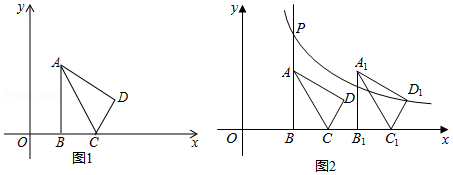
如图，若正方形ABCD的四个顶点恰好分别在四条平行线l1、l-优题课

如图，若正方形ABCD的四个顶点恰好分别在四条平行线l₁、l₂、l₃、l₄上，设这四条直线中相邻两条之间的距离依次为h₁、h₂、h₃(h₁＞0，h₂＞0，h₃＞0)．

（1）求证：h₁＝h₃；
（2）现在平面直角坐标系内有四条直线l₁、l₂、l₃、x轴，且l₁∥l₂∥l₃∥x轴，若相邻两直线间的距离为1，2，1，点A（4，4）在l₁，能否在l₂、l₃、x轴上各找一点B、C、D，使以这四个点为顶点的四边形为正方形，若能，请直接写出B、C、D的坐标；若不能，请说明理由。

科目数学题型解答题难度中等

知识点：圆内接四边形的性质

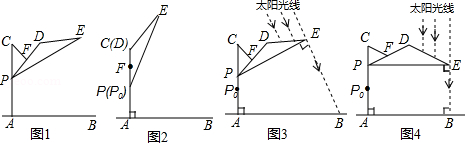
如图1，滑动调节式遮阳伞的立柱 $AC$ 垂直于地面 $AB$ ， $P$ 为立柱上的滑动调节点，伞体的截面示意图为 $ΔPDE$ ， $F$ 为 $PD$ 的中点， $AC = 2.8 m$ ， $PD = 2 m$ ， $CF = 1 m$ ， $∠ DPE = 20 °$ ，当点 $P$ 位于初始位置 $P_{0}$ 时，点 $D$ 与 $C$ 重合（图 $2)$ ．根据生活经验，当太阳光线与 $PE$ 垂直时，遮阳效果最佳．

（1）上午 $10 : 00$ 时，太阳光线与地面的夹角为 $65 °$ （图 $3)$ ，为使遮阳效果最佳，点 $P$ 需从 $P_{0}$ 上调多少距离？（结果精确到 $0.1 m)$

（2）中午 $12 : 00$ 时，太阳光线与地面垂直（图 $4)$ ，为使遮阳效果最佳，点 $P$ 在（1）的基础上还需上调多少距离？（结果精确到 $0.1 m)$ （参考数据： $\sin 70 ° \approx 0.94$ ， $\cos 70 ° \approx 0.34$ ， $\tan 70 ° \approx 2.75$ ， $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73)$

小红帮弟弟荡秋千（如图 $1)$ ，秋千离地面的高度 $ℎ (m)$ 与摆动时间 $t (s)$ 之间的关系如图2所示．

（1）根据函数的定义，请判断变量 $ℎ$ 是否为关于 $t$ 的函数？

（2）结合图象回答：

①当 $t = 0.7 s$ 时， $ℎ$ 的值是多少？并说明它的实际意义．

②秋千摆动第一个来回需多少时间？

某厂为了检验甲、乙两车间生产的同一款新产品的合格情况（尺寸范围为 $176 mm ~ 185 mm$ 的产品为合格），随机各抽取了20个样品进行检测，过程如下：

收集数据（单位： $mm)$

甲车间：168，175，180，185，172，189，185，182，185，174，192，180，185，178，173，185，169，187，176，180．

乙车间：186，180，189，183，176，173，178，167，180，175，178，182，180，179，185，180，184，182，180，183．

整理数据：

	$165.5 ~ 170.5$	$170.5 ~ 175.5$	$175.5 ~ 180.5$	$180.5 ~ 185.5$	$185.5 ~ 190.5$	$190.5 ~ 195.5$
甲车间	2	4	5	6	2	1
乙车间	1	2	$a$	$b$	2	0

分析数据：

车间	平均数	众数	中位数	方差
甲车间	180	185	180	43.1
乙车间	180	180	180	22.6

应用数据：

（1）计算甲车间样品的合格率．

（2）估计乙车间生产的1000个该款新产品中合格产品有多少个？

（3）结合上述数据信息，请判断哪个车间生产的新产品更好，并说明理由．

已知：在 $ΔABC$ 中， $AB = AC$ ， $D$ 为 $AC$ 的中点， $DE ⊥ AB$ ， $DF ⊥ BC$ ，垂足分别为点 $E$ ， $F$ ，且 $DE = DF$ ．求证： $ΔABC$ 是等边三角形．

如图1，在平面直角坐标系 $xOy$ 中，已知 $ΔABC$ ， $∠ ABC = 90 °$ ，顶点 $A$ 在第一象限， $B$ ， $C$ 在 $x$ 轴的正半轴上 $(C$ 在 $B$ 的右侧）， $BC = 2$ ， $AB = 2 \sqrt{3}$ ， $ΔADC$ 与 $ΔABC$ 关于 $AC$ 所在的直线对称．

（1）当 $OB = 2$ 时，求点 $D$ 的坐标；

（2）若点 $A$ 和点 $D$ 在同一个反比例函数的图象上，求 $OB$ 的长；

（3）如图2，将（2）中的四边形 $ABCD$ 向右平移，记平移后的四边形为 $A_{1} B_{1} C_{1} D_{1}$ ，过点 $D_{1}$ 的反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象与 $BA$ 的延长线交于点 $P$ ．问：在平移过程中，是否存在这样的 $k$ ，使得以点 $P$ ， $A_{1}$ ， $D$ 为顶点的三角形是直角三角形？若存在，请直接写出所有符合题意的 $k$ 的值；若不存在，请说明理由．