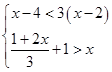如图，抛物线y＝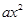
＋bx＋c的顶点为C（0，－
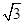），与x轴交于点A、B，连接AC、BC，得等边△ABC. T点从B点出发，以每秒1个单位的速度向点A运动，同时点S从点C出发，以每秒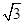个单位的速度向y轴负方向运动，TS交射线BC于点D，当点T到达A点时，点S停止运动. 设运动时间为t秒.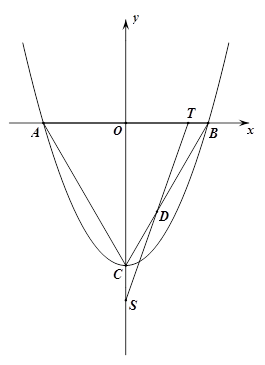
（1）求二次函数的解析式；
（2）设△TSC的面积为S，求S关于t的函数解析式；
（3）以点T为圆心，TB为半径的圆与射线BC交于点E，试说明：在点T运动的过程中，线段ED的长是一定值，并求出该定值.
某公司专销产品
，第一批产品上市40天内全部售完．该公司对第一批产品上市后的市场销售情况进行了跟踪调查，调查结果如图所示，其中图1中的折线表示的是市场日销售量与上市时间的关系；图2中的折线表示的是每件产品的销售利润与上市时间的关系．
（1）试写出第一批产品的市场日销售量
与上市时间的关系式；
（2）第一批产品上市后，哪一天这家公司市场日销售利润最大？最大利润是多少万元？（说明理由）
直线a、b相交于点A，C、E分别是直线b、a上两点且BC⊥a，DE⊥b，点M、N是中点．求证：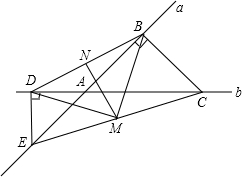
（1）DM=BM；
（2）MN⊥BD．
老师给初二(10)班同学分练习本,如果每人分到4本,那么还剩24本；如果每人分到5本,那么只有一个同学分到但不足5本。求这个班的人数
如图，已知 △ABC、△ADE均为等边三角形，点D是BC延长线上一点，连结CE，求证：BD=CE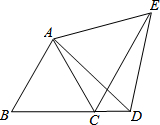
解不等式组，并在数轴上表示解集。
（1）
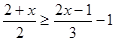（2）