如图，抛物线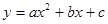
经过点A
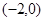、B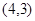
两点，且当x=3和x=-3时，这条抛物线上对应点的纵坐标相等，经过点C
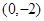的直线
与x轴平行．
（1）求这条抛物线的解析式；
（2）若D是直线上的一个动点，求使△DAB的周长最小时点D的坐标；
（3）以这条抛物线上的任意一点P为圆心，PO的长为半径作⊙P，试判断⊙P与直线的位置关系，并说明理由．
如图，在四边形ABCD中，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，AB=4，AD=6，求AC的长．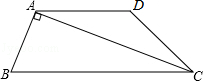
已知反比例函数y1=
的图象与一次函数y2=ax+b的图象交于点A（1，4）和点B（m，-2）．
（1）求这两个函数的关系式；
（2）观察图象，写出使得y1＜y2成立的自变量x的取值范围；
（3）在x轴的正半轴上存在一点P，且△ABP的面积是6，请直接写出点P的坐标．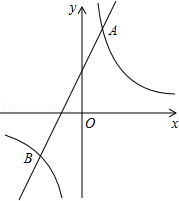
某产品生产车间有工人10名．已知每名工人每天可生产甲种产品12个或乙种产品10个，且每生产一个甲种产品可获利润100元，每生产一个乙种产品可获利润180元．在这10名工人中，如果要使此车间每天所获利润不低于15600元，你认为至少要派多少名工人去生产乙种产品才合适．
已知a2-2a-2=0，求代数式（1-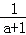
）÷
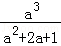的值．
解方程：x2-4x+2=0．