某学校为丰富大课间体育活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么?”,整理收集到的数据,绘制成如图所示的统计图.
(1)学校采用的调查方式是 ;
(2)写出喜欢“踢毽子”的学生人数,并在图中将“踢毽子”部分的图形补充完整;
(3)该校共有800名学生,请估计喜欢“跳绳”的学生人数.
在平面直角坐标系中按下列要求作图.
(1)作出三象限中的小鱼关于x轴的对称图形;
(2)将(1)中得到的图形再向右平移6个单位长度.
购进某种干果,由于销售状况良好,超市又用9000元第二次购进该干果,但第二次的进价比第一次的提髙了20%,第二次购进干果数量是第一次的2倍还多300千克.
(1)求该干果的第一次进价是每千克多少元?
(2)百姓超市按每千克9元的价格出售,当大部分干果售出后,余下的按售价的8折售完,若两次销售这种干果的利润不少于5820元,则最多余下多少千克干果按售价的8折销售.
李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.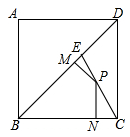
(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
先化简,再求值: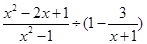 ,其中x=0.
,其中x=0.