在平面直角坐标系中,我们定义直线 为抛物线 、 、 为常数, 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在 轴上的三角形为其“梦想三角形”.
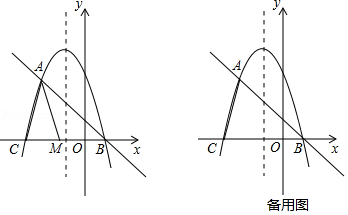
已知抛物线 与其“梦想直线”交于 、 两点(点 在点 的左侧),与 轴负半轴交于点 .
(1)填空:该抛物线的“梦想直线”的解析式为 ,点 的坐标为 ,点 的坐标为 ;
(2)如图,点 为线段 上一动点,将 以 所在直线为对称轴翻折,点 的对称点为 ,若 为该抛物线的“梦想三角形”,求点 的坐标;
(3)当点 在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点 ,使得以点 、 、 、 为顶点的四边形为平行四边形?若存在,请直接写出点 、 的坐标;若不存在,请说明理由.
某服装柜在销售中发现:进货价为每件50元,销售价为每件90元的某品牌服装平均每天可售出20件,现商场决定采取适当的降价措施,扩大销售量,增加盈利,经市场调查发现:如果每件服装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种服装盈利l200元,同时又要使顾客得到较多的实惠,那么每件服装应降价多少元?
如图所示:在平面直角坐标系中,网格中每一个小正方形的边长为l个单位长度;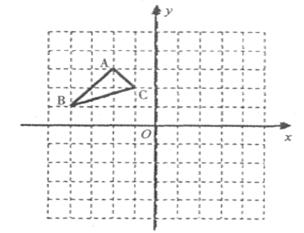

(1)将△ABC向 轴正方向平移5个单位得△A1B1C1,
轴正方向平移5个单位得△A1B1C1,
(2)将△ABC再以原点O为旋转中心,旋转l80°得△A2B2C2,
(3)将△ABC再以点B为旋转中心,顺时针旋转90°得△A3B3C3,画出平移和旋转后的图形,并标明对应字母.
若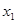 ,
,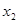 是方程
是方程 的两个根.
的两个根.
(1)求 和
和 的值.
的值.
(2)求 的值.
的值.
(3)求 的值.
的值.
解方程(每题4+6分,共10分)
(1)
(2)先化简,再求值: ,其中x为方程
,其中x为方程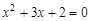 的根.
的根.
如图,抛物线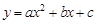 交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3).点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线
交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3).点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线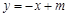 过点C,交y轴于D点.
过点C,交y轴于D点.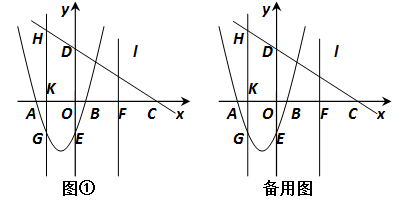
(1)求抛物线的函数表达式;
(2)点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于点G,求线段HG长度的最大值;
(3)在直线l上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.