一个三角形的三边长分别为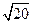 厘米、
厘米、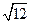 厘米、
厘米、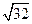 厘米,求三角乡的周长和面积。
厘米,求三角乡的周长和面积。
2x2+2x-1=0(配方法)
2x2-3x-5=0
问题再现
现实生活中,镶嵌图案在地面、墙面乃至于服装面料设计中随处可见.在八年级课题学习“平面图形的镶嵌”中,对于单种多边形的镶嵌,主要研究了三角形、四边形、正六边形的镶嵌问题.今天我们把正多边形的镶嵌作为研究问题的切入点,提出其中几个问题,共同来探究.
我们知道,可以单独用正三角形、正方形或正六边形镶嵌平面.如右图中,用正方形镶嵌平面,可以发现在一个顶点O周围围绕着4个正方形的内角.
试想:如果用正六边形来镶嵌平面,在一个顶点周围应该围绕着 个
正六边形的内角.
问题提出
如果我们要同时用两种不同的正多边形镶嵌平面,可能设计出几种不同的组合方案?
问题解决
猜想1:是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌?
分析:我们可以将此问题转化为数学问题来解决.从平面图形的镶嵌中可以发现,解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点.具体地说,就是在镶嵌平面时,一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角.
验证1:在镶嵌平面时,设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意,可得方程: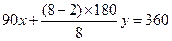 ,整理得:
,整理得: ,
,
我们可以找到惟一一组适合方程的正整数解为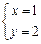 .
.
结论1:镶嵌平面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌.
猜想2:是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.
验证2:
结论2:
上面,我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况,仅仅得到了一部分组合方案,相信同学们用同样的方法,一定会找到其它可能的组合方案.
问题拓广
请你仿照上面的研究方式,探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案,并写出验证过程.
猜想3: .
验证3:
结论3:
.
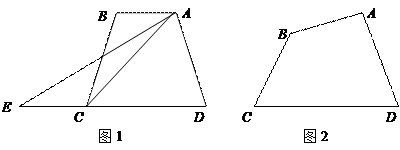
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.如,平行四边形的一条对角线所在的直线就是平行四边形的一条面积等分线.
(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的是_______;
(2)如图1,梯形ABCD中,AB∥DC,如果延长DC到E,使CE=AB,连接AE,那么有S梯形ABCD =S△ADE.请你给出这个结论成立的理由,并过点A作出梯形ABCD的面积等分线(不写作法,保留作图痕迹);
(3)如图2,四边形ABCD中,AB与CD不平行,S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并给出说明;若不能,说明理由.