如图:在直角坐标系中,以点A(3,0)为圆心,以5为半径的圆与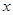 轴相交于B、C两点,与
轴相交于B、C两点,与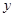 轴相交于D、E两点.
轴相交于D、E两点.若抛物线
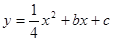 经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?
经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?过点E的直线
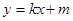 交
交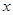 轴于F(
轴于F(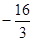 ,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;
,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;探索:是否能在(1)中的抛物线上找到一点Q,使直线BQ与
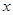 轴正方向所夹锐角的正切值等于
轴正方向所夹锐角的正切值等于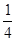 ?,若能,请直接写出Q点坐标;若不能,请说明理由. (4分)
?,若能,请直接写出Q点坐标;若不能,请说明理由. (4分)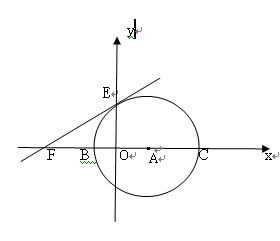
如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.
求证:AD=EC;
当∠BAC=90º时,求证:四边形ADCE是菱形;
在(2)的条件下,若AB=AO,且OD=
 ,求菱形ADCE的周长.
,求菱形ADCE的周长.
市园林处为了对一段公路进行绿化,计划购买A、B两种风景树共900棵。若购买A树x棵,所需总费用y元. B两种树的相关信息如下表:
A、
求y与x之间的函数关系式.
若购树的总费用不超过82000元,则购A种树不少于多少棵?
若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两
种树各多少棵?此时最低费用为多少?
如图: 在△AEB和△ADC中,给出以下四个论断:(1)AB=AC;(2)AD=AE;
(3)AM=AN;(4)AD⊥DC,AE⊥BE.以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中,使之组成一个真命题,并写出证明过程。
如图,在△AEB和△ADC中,已知:______________.
求证: _______.
证明:
在一个透明的袋子里,装有相同的四个小球,其上面分别标有数字-1,1,2,3.现从中任意摸出一个小球,将上面的数字作为点A的横坐标,不放回再从中摸出一个小球,将其上面的数字作为A点的纵坐标.用树状图或列表法写出A点坐标的所有可能性;
求点A在直线
 上的概率;
上的概率;求点A的横坐标、纵坐标之和是偶数的概率.