甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．-优题课

甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．

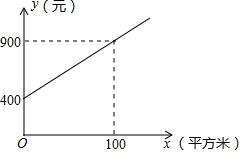
甲公司方案：每月的养护费用 $y$ （元 $)$ 与绿化面积 $x$ （平方米）是一次函数关系，如图所示．

乙公司方案：绿化面积不超过1000平方米时，每月收取费用5500 元；绿化面积超过1000平方米时，每月在收取5500元的基础上，超过部分每平方米收取4元．

（1）求如图所示的 $y$ 与 $x$ 的函数解析式：（不要求写出定义域）；

（2）如果某学校目前的绿化面积是1200平方米，试通过计算说明：选择哪家公司的服务，每月的绿化养护费用较少．

科目数学题型解答题难度中等

知识点：一次函数的应用

先化简，再求值： ${(x + y)}^{2} + (x + y) (x - y) - 2 x^{2}$ ，其中 $x = \sqrt{2}$ ， $y = \sqrt{3}$ ．

在平面直角坐标系中，正方形 $ABCD$ 的四个顶点坐标分别为 $A (- 2, 4)$ ， $B (- 2, - 2)$ ， $C (4, - 2)$ ， $D (4, 4)$ ．

（1）填空：正方形的面积为　　；当双曲线 $y = \frac{k}{x} (k \neq 0)$ 与正方形 $ABCD$ 有四个交点时， $k$ 的取值范围是：　　；

（2）已知抛物线 $L : y = a {(x - m)}^{2} + n (a > 0)$ 顶点 $P$ 在边 $BC$ 上，与边 $AB$ ， $DC$ 分别相交于点 $E$ ， $F$ ，过点 $B$ 的双曲线 $y = \frac{k}{x} (k \neq 0)$ 与边 $DC$ 交于点 $N$ ．

①点 $Q (m, - m^{2} - 2 m + 3)$ 是平面内一动点，在抛物线 $L$ 的运动过程中，点 $Q$ 随 $m$ 运动，分别求运动过程中点 $Q$ 在最高位置和最低位置时的坐标；

②当点 $F$ 在点 $N$ 下方， $AE = NF$ ，点 $P$ 不与 $B$ ， $C$ 两点重合时，求 $\frac{BE}{BP} - \frac{CF}{CP}$ 的值；

③求证：抛物线 $L$ 与直线 $x = 1$ 的交点 $M$ 始终位于 $x$ 轴下方．

已知：在矩形 $ABCD$ 中， $E$ ， $F$ 分别是边 $AB$ ， $AD$ 上的点，过点 $F$ 作 $EF$ 的垂线交 $DC$ 于点 $H$ ，以 $EF$ 为直径作半圆 $O$ ．

（1）填空：点 $A$ 　　（填“在”或“不在” $) ⊙ O$ 上；当 $\hat{AE} = \hat{AF}$ 时， $\tan ∠ AEF$ 的值是　　；

（2）如图1，在 $ΔEFH$ 中，当 $FE = FH$ 时，求证： $AD = AE + DH$ ；

（3）如图2，当 $ΔEFH$ 的顶点 $F$ 是边 $AD$ 的中点时，求证： $EH = AE + DH$ ；

（4）如图3，点 $M$ 在线段 $FH$ 的延长线上，若 $FM = FE$ ，连接 $EM$ 交 $DC$ 于点 $N$ ，连接 $FN$ ，当 $AE = AD$ 时， $FN = 4$ ， $HN = 3$ ，求 $\tan ∠ AEF$ 的值．

$HW$ 公司2018年使用自主研发生产的“ $QL$ ”系列甲、乙、丙三类芯片共2800万块，生产了2800万部手机，其中乙类芯片的产量是甲类芯片的2倍，丙类芯片的产量比甲、乙两类芯片产量的和还多400万块．这些“ $QL$ ”芯片解决了该公司2018年生产的全部手机所需芯片的 $10 %$ ．

（1）求2018年甲类芯片的产量；

（2） $HW$ 公司计划2020年生产的手机全部使用自主研发的“ $QL$ ”系列芯片．从2019年起逐年扩大“ $QL$ ”芯片的产量，2019年、2020年这两年，甲类芯片每年的产量都比前一年增长一个相同的百分数 $m %$ ，乙类芯片的产量平均每年增长的百分数比 $m %$ 小1，丙类芯片的产量每年按相同的数量递增 $. 2018$ 年到2020年，丙类芯片三年的总产量达到1.44亿块．这样，2020年的 $HW$ 公司的手机产量比2018年全年的手机产量多 $10 %$ ，求丙类芯片2020年的产量及 $m$ 的值．

如图，点 $O$ 是线段 $AH$ 上一点， $AH = 3$ ，以点 $O$ 为圆心， $OA$ 的长为半径作 $⊙ O$ ，过点 $H$ 作 $AH$ 的垂线交 $⊙ O$ 于 $C$ ， $N$ 两点，点 $B$ 在线段 $CN$ 的延长线上，连接 $AB$ 交 $⊙ O$ 于点 $M$ ，以 $AB$ ， $BC$ 为边作 $▱ ABCD$ ．

（1）求证： $AD$ 是 $⊙ O$ 的切线；

（2）若 $OH = \frac{1}{3} AH$ ，求四边形 $AHCD$ 与 $⊙ O$ 重叠部分的面积；

（3）若 $NH = \frac{1}{3} AH$ ， $BN = \frac{5}{4}$ ，连接 $MN$ ，求 $OH$ 和 $MN$ 的长．