已知在平面直角坐标系xOy中（如图），已知抛物线yx2bxc-优题课

游客

题文

已知在平面直角坐标系 $xOy$ 中（如图），已知抛物线 $y = - x^{2} + bx + c$ 经过点 $A (2, 2)$ ，对称轴是直线 $x = 1$ ，顶点为 $B$ ．

（1）求这条抛物线的表达式和点 $B$ 的坐标；

（2）点 $M$ 在对称轴上，且位于顶点上方，设它的纵坐标为 $m$ ，联结 $AM$ ，用含 $m$ 的代数式表示 $∠ AMB$ 的余切值；

（3）将该抛物线向上或向下平移，使得新抛物线的顶点 $C$ 在 $x$ 轴上．原抛物线上一点 $P$ 平移后的对应点为点 $Q$ ，如果 $OP = OQ$ ，求点 $Q$ 的坐标．

科目数学题型解答题难度中等

知识点：锐角三角函数的定义二次函数图象上点的坐标特征二次函数图象与几何变换待定系数法求二次函数解析式二次函数综合题线段垂直平分线的性质

登录免费查看答案和解析

相关试题

一只箱子里共有3个球，其中2个白球，1个红球，它们除颜色外均相同．
（1）从箱子中任意摸出一个球是白球的概率是多少？
（2）从箱子中任意摸出一个球，不将它放回箱子，搅匀后再摸出一个球，用列表或画树状的方法求两次摸出的球都是白球的概率．

解不等式组，并把不等式组的解集在数轴上表示出来。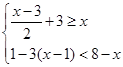

先化简，再求值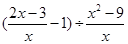：，其中．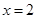

如图，在平面直角坐标系中，点A，B的坐标分别为（﹣3，0），（0，6）．动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从B出发，沿射线BO方向以每秒2个单位的速度运动，以CP，CO为邻边构造平行四边形PCOD，在线段OP延长线上取点E，使PE=AO，设点P运动的时间为t秒．

（1）直接写出当点C运动到线段OB的中点时，求t的值及点E的坐标．
（2）当点C在线段OB上运动时，四边形ADEC的面积为S．
①求证：四边形ADEC为平行四边形．
②写出s与t的函数关系式，并求出t的取值范围．
（3）是否存在某一时刻，使OC是PC的一半？若存在，求出t的值，若不存在，请说明理由．

某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个，摆放在迎宾大道两侧．已知搭配一个A种造型需甲种花卉8盆，乙种花卉4盆；搭配一个B种造型需甲种花卉5盆，乙种花卉9盆．
（l）某校2015届九年级某班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来；
（2）若搭配一个A种造型的成本是200元，搭配一个B种造型的成本是360元，试说明（1）中哪种方案成本最低，最低成本是多少元？

试卷网试题网古诗词网作文网范文网