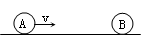
如图所示，一对半径均为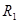
的金属板M、N圆心正对平行放置，两板距离为
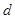，N板中心镀有一层半径为
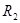的圆形锌金属薄膜，
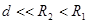，两板之间电压为
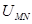，两板之间真空且可视为匀强电场。N板受到某种单色光照射后锌金属薄膜表面会发射出最大速率为
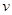，方向各异的电子，已知电子的电荷量为
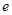，质量为
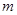，每秒稳定发射
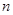个电子。电子在板间运动过程中无碰撞且不计电子的重力和电子间相互作用，电子到达M板全部被吸收。M板右侧串联的电流表可以测量到通过M板的电流
。试求：
（1）当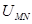取什么值时，始终为零；
（2）当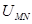取什么值时，存在一个最大值，并求这个最大值；
（3）请利用（1）（2）的结论定性画出随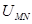变化的图像。
2011年3月11日13时45分，日本发生9级地震并引发海啸，造成了福山核电站核泄露。日本自卫队16日出动美制CH-47D大型运输直升机提取海水为福岛第一核电站三号反应堆“泼水降温”。已知每架直升机每次从海中提取的水量为7.5吨,提水后，设直升机从悬停状态竖直向上匀加速，经过5秒钟直升机拖着水桶上升的速度达到4m/s。(取g=10m/s2)
（1）求此时直升机向上运动的距离是多少
（2）直升机向上运动时绳索对水桶的拉力是多大
如图所示，甲车的质量是2 kg，静止在光滑水平面上，上表面光滑，右端放一个质量为1 kg的小物体.乙车质量为4 kg，以5 m/s的速度向左运动，与甲车碰撞以后甲车获得8 m/s的速度，物体滑到乙车上.若乙车足够长，上表面与物体的动摩擦因数为0.2，则物体在乙车上表面滑行多长时间相对乙车静止?(g取10 m/s2)
如图所示，A、B是两块质量均为m的木块，它们之间的滑动摩擦因数为μ，B与地面间的滑动摩擦因数也为μ，现对A施加一个水平向右的拉力F，可使A向右，B向左都做匀速直线运动.若滑轮处的摩擦不计，则F的大小等于多少？
如图所示，一平直的传送带以速度v=2m/s匀速运动，传送带把A处的工件运送到B处，A、B相距L=10m．从A处把工件无初速地放到传送带上，经过时间t=6s能传送到B处．求：
（1）工件在传送带上做匀加速运动的时间；
（2）工件做匀加速运动的加速度大小．
在光滑水平地面上有两个相同的弹性小球A、B，质量都为m.现B球静止，A球向B球运动，发生正碰．已知碰撞过程中总机械能守恒，两球压缩最紧时的弹性势能为Ep，求：碰前A球的速度大小等于多少？