某中学组织中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题: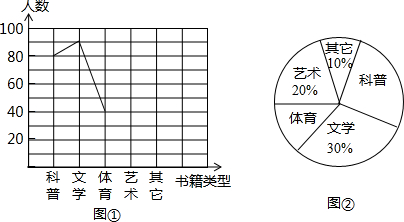
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A B
B C
C .
.
(1)在图中画出△A B
B C
C ;
;
(2)写出点A 、B
、B 、C
、C 的坐标;
的坐标;
(3)在 轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
小红和小凤两人在解关于 、
、 的方程组
的方程组 时,小红只因看错了系数
时,小红只因看错了系数 ,得到方程组的解为
,得到方程组的解为 ;小凤只因看错了系数
;小凤只因看错了系数 ,得到方程组的解为
,得到方程组的解为 ;求
;求 、
、 的值和原方程组的解.
的值和原方程组的解.
定义运算:对于任意实数 、
、 ,都有
,都有

 =
= ,等式右边是通常的加法、减法、及乘法运算,比如:2
,等式右边是通常的加法、减法、及乘法运算,比如:2 5=2×(2-5)+1=2×(-3)+1=-6+1=-5.若3
5=2×(2-5)+1=2×(-3)+1=-6+1=-5.若3
 的值小于13,求
的值小于13,求 的取值范围,并在如图所示的数轴上表示出来.
的取值范围,并在如图所示的数轴上表示出来.
如图,AB∥CD,直线MN分别交AB、CD于E、F,EG平分∠AEN交CD于点G,∠MEB=80°,求∠EGD的度数.