某中学组织中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题: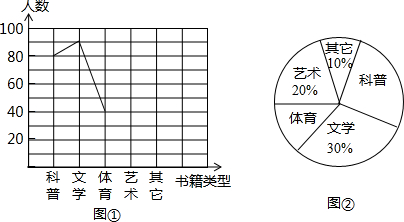
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
如图,反比例函数 的图象与一次函数 的图象交于 , 两点,点 和点 的横坐标分别为1和 ,这两点的纵坐标之和为1.
(1)求反比例函数的表达式与一次函数的表达式;
(2)当点 的坐标为 时,求 的面积.
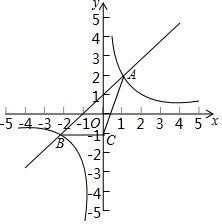
如图,以 为底边的等腰 ,点 , , 分别在 , , 上,且 , ,延长 至点 ,使得 .
(1)求证:四边形 为平行四边形;
(2)当 , 时,求 , 两点间的距离.

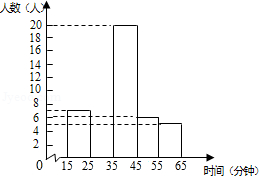
某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
频率分布表
|
组别 |
分组 |
频数 |
频率 |
|
1 |
|
7 |
0.14 |
|
2 |
|
|
0.24 |
|
3 |
|
20 |
0.40 |
|
4 |
|
6 |
|
|
5 |
|
5 |
0.10 |
注:这里的 表示大于等于15同时小于25.
(1)求被调查的学生人数;
(2)直接写出频率分布表中的 和 的值,并补全频数分布直方图;
(3)若该校共有学生500名,则平均每天课外阅读的时间不少于35分钟的学生大约有多少名?
某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
(1)求每位“快递小哥”的日收入 (元 与日派送量 (件 之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?

如图,直线 与 轴、 轴分别交于 , 两点,抛物线 与直线 分别交 轴的正半轴于点 和第一象限的点 ,连接 ,得 为坐标原点).若抛物线与 轴正半轴交点为点 ,设 是点 , 间抛物线上的一点(包括端点),其横坐标为 .
(1)直接写出点 的坐标和抛物线的解析式;
(2)当 为何值时, 面积 取得最小值和最大值?请说明理由;
(3)求满足 的点 的坐标.
