已知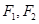 为椭圆
为椭圆
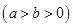 的左、右焦点,
的左、右焦点,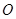 是坐标原点,过
是坐标原点,过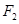 作垂直于
作垂直于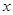 轴的直线
轴的直线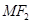 交椭圆于
交椭圆于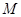
 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过左焦点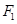 的直线
的直线 与椭圆
与椭圆 交于
交于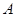 、
、 两点,若
两点,若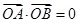 ,求直线
,求直线 的方程.
的方程.
(本小题满分14分)已知函数 ,
,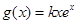 (
(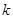 为常数,
为常数,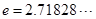 是自然对数的底数),
是自然对数的底数),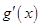 为
为 的导函数,且
的导函数,且 .
.
(1)求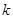 的值;
的值;
(2)对任意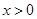 ,证明:
,证明: ;
;
(3)若对所有的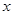 ≥0,都有
≥0,都有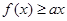 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知椭圆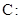
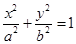 (
(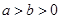 )的右焦点
)的右焦点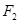 是抛物线
是抛物线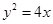 的焦点,过点
的焦点,过点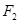 垂直于
垂直于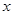 轴的直线被椭圆
轴的直线被椭圆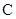 所截得的线段长度为
所截得的线段长度为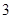 .
.
(1)求椭圆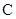 的方程;
的方程;
(2)设动直线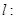
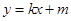 与椭圆
与椭圆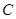 有且只有一个公共点
有且只有一个公共点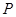 ,且与直线
,且与直线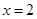 相交于点
相交于点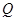 .请问:在
.请问:在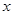 轴
轴
上是否存在定点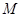 ,使得
,使得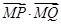 为定值?若存在,求出点
为定值?若存在,求出点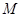 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分12分)已知函数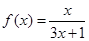 ,数列
,数列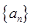 满足
满足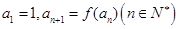 .
.
(1)求数列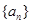 的通项公式;
的通项公式;
(2)记 ,证明:
,证明: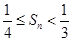 .
.
(本小题满分12分)如图,平面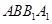 为圆柱
为圆柱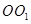 的轴截面,点
的轴截面,点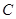 为底面圆周上异于
为底面圆周上异于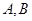 的任意一点.
的任意一点.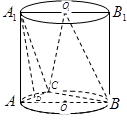
(1)求证: 平面
平面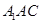 ;
;
(2)若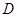 为
为 的中点,求证:
的中点,求证: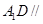 平面
平面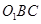 .
.
(本小题满分12分)某校高三文科(1)班学生参加“大联考”,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布区间为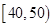 ,
,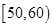 ,
,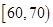 ,
,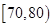 ,
,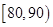 ,
,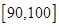 ,现已知成绩落在
,现已知成绩落在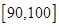 的有
的有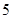 人.
人.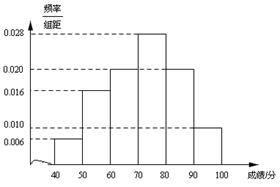
(1)求该校高三文科(1)班参加“大联考”的总人数;
(2)根据频率分布直方图,估计该班此次数学成绩的平均分(可用中值代替各组数据的平均值);
(3)现要从成绩在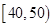 和
和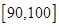 的学生中共选
的学生中共选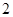 人参加某项座谈会,求
人参加某项座谈会,求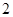 人来自于同一分数段的概
人来自于同一分数段的概
率.