已知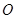 为坐标原点,
为坐标原点,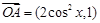 ,
,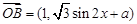 (
(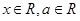 ,
,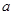 是常数),若
是常数),若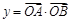 .
.
(1)求 关于
关于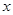 的函数关系式
的函数关系式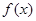 ;
;
(2)若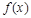 的最大值为
的最大值为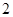 ,求
,求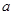 的值;
的值;
(3)利用(2)的结论,用“五点法”作出函数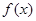 在长度为一个周期的闭区间上的简图,并指出函数
在长度为一个周期的闭区间上的简图,并指出函数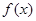 的单调区间
的单调区间
(本题满分15分)已知a∈R,函数f (x) =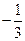 x3 +
x3 +  ax2 + 2ax (x∈R).(Ⅰ)当a = 1时,求函数f (x)的单调递增区间;(Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由;(Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.
ax2 + 2ax (x∈R).(Ⅰ)当a = 1时,求函数f (x)的单调递增区间;(Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由;(Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.
(本小题满分14分)
已知函数 对于任意
对于任意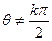 (
(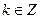 ),都有式子
),都有式子 成立(其中
成立(其中 为常数).
为常数).
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)利用函数 构造一个数列,方法如下:
构造一个数列,方法如下:
对于给定的定义域中的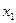 ,令
,令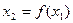 ,
, ,…,
,…,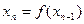 ,…
,…
在上述构造过程中,如果 (
(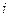 =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止.
(ⅰ)如果可以用上述方法构造出一个常数列,求 的取值范围;
的取值范围;
(ⅱ)是否存在一个实数 ,使得取定义域中的任一值作为
,使得取定义域中的任一值作为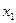 ,都可用上述方法构造出一个无穷数列
,都可用上述方法构造出一个无穷数列 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(ⅲ)当 时,若
时,若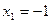 ,求数列
,求数列 的通项公式.
的通项公式.
如图所示,已知圆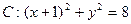 ,定点
,定点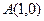 ,
, 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点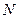 在
在 上,且满足
上,且满足 ,
, ,点
,点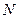 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ) 求曲线 的方程;
的方程;
(Ⅱ) 若点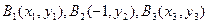 在曲线
在曲线 上,线段
上,线段 的垂直平分线为直线
的垂直平分线为直线 ,且
,且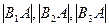 成等差数列,求
成等差数列,求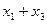 的值,并证明直线
的值,并证明直线 过定点;
过定点;
(Ⅲ)若过定点 (0,2)的直线交曲线
(0,2)的直线交曲线 于不同的两点
于不同的两点 、
、 (点
(点 在点
在点 、
、 之间),且满足
之间),且满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分14分)
如图,三棱锥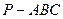 中,
中, ,
, .
.
(Ⅰ)求证: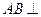 平面
平面 ;
; (Ⅱ)若
(Ⅱ)若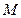 为线段
为线段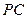 上的点,设
上的点,设 ,问
,问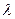 为何值时能使
为何值时能使
直线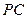
 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
(本小题满分12分)
已知函数 ,在函数
,在函数 图像上一点
图像上一点 处切线的斜率为3.
处切线的斜率为3.
(Ⅰ)若函数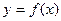 在
在 时有极值,求
时有极值,求 的解析式;
的解析式;
(Ⅱ)若函数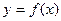 在区间
在区间 ,
, 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.