某企业生产
两种产品，每生产
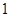吨产品所需的劳动力、煤、电消耗及利润如下表：
| 产品品种 |
劳动力（个） |
煤（吨） |
电（千瓦时） |
利润（万元） |
 产品 |
4 |
9 |
3 |
7 |
 产品 |
5 |
4 |
10 |
12 |
因条件限制，该企业仅有劳动力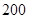
个，煤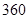
吨，供电局最多供电
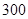千瓦时，试问该企业生产两种产品各多少吨时能获得最大利润？并求最大利润．
设离散型随机变量X的概率分布为
| X |
0 |
1 |
2 |
3 |
4 |
| P |
0.2 |
0.1 |
0.1 |
0.3 |
m |
求：（1）2X+1的概率分布；
（2）|X-1|的概率分布.
某校高三年级某班的数学课外活动小组中有6名男生，4名女生，从中选出4人参加数学竞赛考试，用X表示其中的男生人数，求X的概率分布.
一袋中装有编号为1，2，3，4，5，6的6个大小相同的球，现从中随机取出3个球，以X表示取出的最大号码.
（1）求X的概率分布；
（2）求X＞4的概率.
已知等腰Rt△ABC中，∠C=90°.
（1）在线段BC上任取一点M，求使∠CAM＜30°的概率；
（2）在∠CAB内任作射线AM，求使∠CAM＜30°的概率.
假设你家订了一份报纸，送报人可能在早上6∶30至7∶30之间把报纸送到你家，你父亲离开家去工作的时间在早上7∶00至8∶00之间，问你父亲在离开家前能得到报纸（称为事件A）的概率是多少？