如图1,在y轴的正半轴上依次有点A1,A2,…,An,…,A1,A2的坐标分别为(0,1),(0,10),且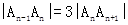 (n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且
(n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且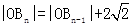 (n=2,3,4,…).
(n=2,3,4,…).
(1)用含n的式子表示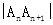 ;
;
(2)用含n 的式子分别表示点An、Bn的坐标;
(3)求四边形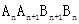 面积的最大值.
面积的最大值.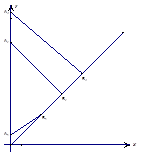
求满足下列条件的曲线方程
(1)经过两点P( ,1),Q(
,1),Q(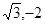 )的椭圆的标准方程.
)的椭圆的标准方程.
(2)与双曲线 有共同的渐近线,且经过点
有共同的渐近线,且经过点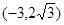 的双曲线的标准方程.
的双曲线的标准方程.
(3)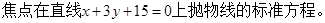
设函数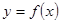 定义在
定义在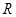 上,对于任意实数
上,对于任意实数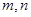 ,恒有
,恒有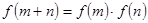 ,且当
,且当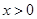 时,
时,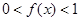
(1)求证: 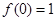 且当
且当 时,
时,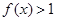
(2)求证: 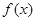 在
在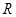 上是减函数;
上是减函数;
(3)设集合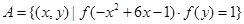 ,
,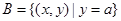 ,且
,且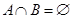 ,
,
求实数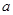 的取值范围。
的取值范围。
某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数: ,其中
,其中 是仪器的月产量。
是仪器的月产量。
(1)将利润 元表示为月产量
元表示为月产量 台的函数;
台的函数;
(2)当月产量为何值时,公司所获得利润最大?最大利润是多少?(总收益=总成本+利润).
已知函数 .
.
(1)证明:不论 为何实数
为何实数 总为增函数
总为增函数
(2)确定 的值, 使
的值, 使 为奇函数;
为奇函数;
(3)当 为奇函数时, 求
为奇函数时, 求 的值域.
的值域.
设f(x)为定义在R上的偶函数,当 时,y=x;当x>2时,y=f(x)的图像时顶点在P(3,4),且过点A.(2,2)的抛物线的一部分
时,y=x;当x>2时,y=f(x)的图像时顶点在P(3,4),且过点A.(2,2)的抛物线的一部分
(1)写出函数f(x)在 上的解析式;
上的解析式;
(2)在下面的直角坐标系中直接画出函数f(x)的图像;
(3)写出函数f(x)值域