如图,已知A(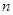 ,-2),B(1,4)是一次函数
,-2),B(1,4)是一次函数 的图象和反比例函数y=
的图象和反比例函数y= 的图象的两个交点,直线AB与
的图象的两个交点,直线AB与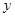 轴交于点C..
轴交于点C..
求反比例函数和一次函数的关系式;
求△AOC的面积
观察图象,直接写出不等式
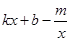 <0的解集.
<0的解集.
如图,在网格图中建立平面直角坐标系,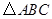 的顶点坐标为
的顶点坐标为 、
、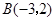 、
、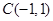 .
.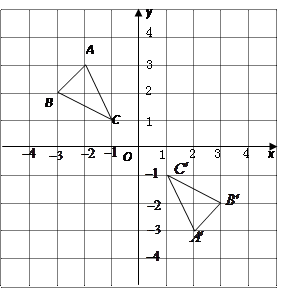
(1)若将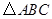 向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的
向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的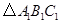 ;
;
(2)画出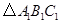 绕C1顺时针方向旋转900后得到的
绕C1顺时针方向旋转900后得到的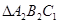 ;
;
(3)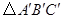 与
与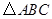 是中心对称图形,请写出对称中心的坐标:;并计算
是中心对称图形,请写出对称中心的坐标:;并计算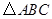 的面积:.
的面积:.
(4)在坐标轴上是否存在P点,使得△PAB与△CAB的面积相等,若有,则求出点P的坐标.
先化简,再求值: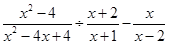 ,其中x=2-
,其中x=2-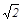 .
.
如图,已知二次函数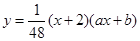 的图象过点
的图象过点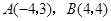 .
.
(1)求二次函数的解析式;
(2)求证: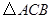 是直角三角形;
是直角三角形;
(3)若点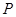 在第二象限,且是抛物线上的一动点,过点
在第二象限,且是抛物线上的一动点,过点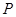 作
作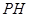 垂直
垂直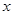 轴于点
轴于点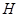 ,试探究是否存在以
,试探究是否存在以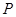 、
、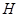 、
、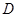 为顶点的三角形与
为顶点的三角形与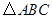 相似?若存在,求出
相似?若存在,求出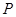 点的坐标.若不存在,请说明理由.
点的坐标.若不存在,请说明理由.
如本题图1,在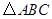 中,
中,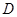 、
、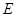 、
、 分别为三边的中点,
分别为三边的中点,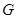 点在边
点在边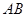 上,
上,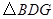 与四边形
与四边形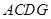 的周长相等,设
的周长相等,设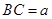 、
、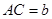 、
、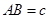 .
.
(1)求线段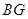 的长(用含
的长(用含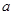 、
、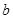 、
、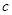 的代数式表示);
的代数式表示);
(2)求证: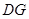 平分
平分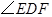 ;
;
(3)连接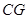 ,如本题图2,若
,如本题图2,若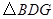 与
与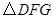 相似,求证:
相似,求证: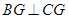 .
.
如图,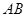 是
是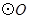 的弦,
的弦,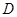 为半径
为半径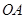 的中点,过
的中点,过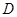 作
作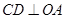 交弦
交弦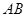 于点
于点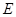 ,交
,交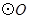 于点
于点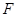 ,且
,且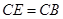 .
.
(1)求证: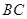 是
是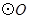 的切线;
的切线;
(2)连接 、
、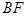 ,求
,求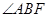 的度数;
的度数;