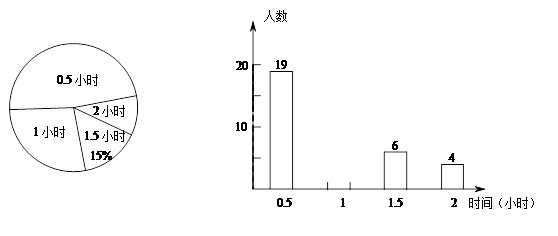
随着“微博潮”的流行，初中学生也开始忙着“织围脖”，某校在上微博的280名学生中随机抽取了部分学生调查他们平常每天上微博的时间，绘制了扇形统计图和频数分布直方图（从左向右依次为第一、二、三、四小组），请根据图中信息，回答下列问题：本次调查共抽取了 ▲ 名学生；将频数分布直方图补充完整；
被调查的学生中上微博时间中位数落在 ▲ 这一小组内
样本中，平均每天上微博的时间为0.5小时这一组的频率是 ▲ ；
请估计该校上微博的学生中，大约有 ▲ 名学生平均每天上微博的时间不少于1小时.
和
的最简公分母是 ．
和
的最简公分母是 ．
，
，
；
，
，
；
；
．
的值是正整数，求整数a．
．