已知椭圆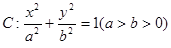 的离心率为
的离心率为 ,其左、右焦点为F1、F2,点P是坐标平面内一点,且
,其左、右焦点为F1、F2,点P是坐标平面内一点,且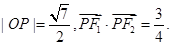 其中O为坐标原点。
其中O为坐标原点。
(I) 求椭圆C的方程;
(II) 如图,过点S(0,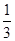 },且斜率为k的动直线l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
},且斜率为k的动直线l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.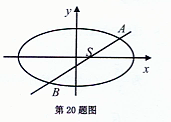
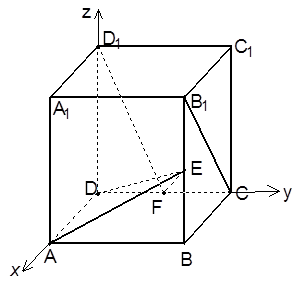
在正方体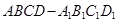 中,如图E、F分别是
中,如图E、F分别是  ,CD的中点,
,CD的中点,
(1)求证: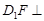 平面ADE;
平面ADE;
(2)cos .
.
命题:已知a、b为实数,若x2+ax+b≤0 有非空解集,则a2- 4b≥0.写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假。
由下列不等式: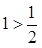 ,
, ,
,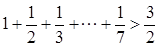 ,
,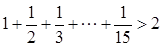 ,
, ,你能得到一个怎样的一般不等式?并加以证明。
,你能得到一个怎样的一般不等式?并加以证明。
据调查统计,某市高二学生中男生的身高X(单位:cm)服从正态分布N(174,9),若该市共有高二男生3 000人,试计算该市高二男生身高在(174,180]范围内的人数.
在二项式 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列
(1)求展开式的常数项; (2)求展开式中二项式系数最大的项;
(3)求展开式中各项的系数和。