设对于任意实数x，不等式
恒成立．
（1）求m的取值范围；
（2）当m取最大值时，解关于x的不等式：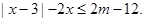
已知
.
(1)当
,
时,若不等式
恒成立,求
的范围；
(2)试判断函数
在
内零点的个数，并说明理由.
某加油站拟造如图所示的铁皮储油罐（不计厚度，长度单位：米），其中储油罐的中间为圆柱形，左右两端均为半球形，
（
为圆柱的高，
为球的半径，
）.假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
千元，半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元.
（1）写出关于的函数表达式，并求该函数的定义域；
（2）求该储油罐的建造费用最小时的的值.
已知复数
（
是虚数单位）在复平面上对应的点依次为
，点
是坐标原点.
（1）若
,求
的值；
（2）若
点的横坐标为
,求
.
已知数列
和
满足：
，其中
为实数，
为正整数.
（1）对任意实数，求证：
不成等比数列；
（2）试判断数列是否为等比数列，并证明你的结论.
（3）设
为数列的前项和.是否存在实数，使得对任意正整数，都有
?若存在，求的取值范围；若不存在，说明理由.
阅读：
已知
、
，
，求
的最小值.
解法如下：
，
当且仅当
，即
时取到等号，
则的最小值为
.
应用上述解法，求解下列问题：
（1）已知
，
，求
的最小值；
（2）已知
，求函数
的最小值；
（3）已知正数
、
、
，
，
求证：
.