抛物线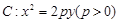 上一点
上一点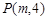 到其焦点的距离为5.
到其焦点的距离为5.
(1)求 与
与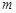 的值;
的值;
(2)若直线 与抛物线
与抛物线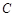 相交于
相交于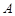 、
、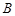 两点,
两点,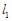 、
、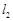 分别是该抛物线在
分别是该抛物线在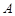 、
、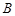 两点处的切线,
两点处的切线,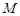 、
、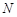 分别是
分别是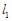 、
、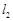 与该抛物线的准线交点,求证:
与该抛物线的准线交点,求证: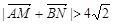
某校举行环保知识大奖赛,比赛分初赛和决赛两部分.初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题连续两次答错的概率为 .(已知甲回答每个问题的正确率相同,并且相互之间没有影响.)
.(已知甲回答每个问题的正确率相同,并且相互之间没有影响.)
(1)求选手甲回答一个问题的正确率.
(2)求选手甲可进入决赛的概率.
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率.
(2)求取出的4个球中恰有1个红球的概率.
如图,电路由电池A,B,C并联组成.电池A,B,C损坏的概率分别是0.3,0.2,0.2,求电路断电的概率.
已知复数z=x+yi(x,y∈R)在复平面上对应的点为M.
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中随机取一个数作为y,求复数z为纯虚数的概率.
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组: 所表示的平面区域内的概率.
所表示的平面区域内的概率.
设函数f(x)=x2+bx+c,其中b,c是某范围内的随机数,分别在下列条件下,求事件A“f(1)≤5且f(0)≤3”发生的概率.
(1)若随机数b,c∈{1,2,3,4}.
(2)已知随机函数Rand( )产生的随机数的范围为{x|0≤x≤1},b,c是算法语句b="4*Rand(" )和c="4*Rand(" )的执行结果.(注:符号“*”表示“乘号”)