如图为河岸一段的示意图.一游泳者站在河岸的A点处，欲前往对岸的C点处，若河宽BC为100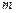
，A、B相距100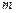，他希望尽快到达C，准备从A步行到E（E为河岸AB上的点），再从E游到C.已知此人步行速度为
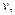游泳速度为
.
（1）设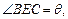
试将此人按上述路线从A到C所需时间T表示为
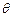的函数，并求自变量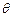的取值范围；
（2）当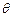为何值时，此人从A经E游到C所需时间T最小，其最小值是多少？
（本小题满分13分）如图，焦点在x轴的椭圆C：
（b > 0），点G（2，0），点P在椭圆上，且PG⊥x轴，连接OP交直线x = 4于点M，连接MG交椭圆于A、B.
（Ⅰ）若G为椭圆右焦点，求|OM|；
（Ⅱ）记直线PA，PB的斜率分别为
，
，求
的取值范围.
（本小题满分13分）已知数列
中，
，
，记
为的前
项的和．设
，
（1）证明：数列
是等比数列；
（2）不等式：
对于一切
恒成立，求实数
的最大值.
（本小题满分12分）某公司举办一次募捐爱心演出，有1000人参加，每人一张门票，每张100元。在演出过程中穿插抽奖活动，第一轮抽奖从这1000张票根中随机抽取10张，其持有者获得价值1000元的奖品，并参加第二轮抽奖活动。第二轮抽奖由第一轮获奖者独立操作按钮，电脑随机产生两个实数
（
），若满足
，电脑显示“中奖”，则抽奖者再次获得特等奖奖金；否则电脑显示“谢谢”，则不中特等奖奖金。
（Ⅰ）已知小明在第一轮抽奖中被抽中，求小明在第二轮抽奖中获奖的概率；
（Ⅱ）设特等奖奖金为a元，求小李参加此次活动收益的期望，若该公司在此次活动中收益的期望值是至少获利70000元，求a的最大值。
（本小题满分12分）如图1，在Rt
中，
，
．
，将
沿
折起到
的位置，使
，如图2．
（Ⅰ）求证： 
平面
；
（Ⅱ）若
，求平面
与平面
所成二面角的大小．
设
,
满足
.
（Ⅰ）求函数
的单调递增区间；
（Ⅱ）设
三内角
所对边分别为
且
，求在
上的值域．