(本小题满分13分)盒中装有7个零件,其中5个是没有使用过的,2个是使用过的.
(Ⅰ)从盒中每次随机抽取1个零件,有放回的抽取3次,求3次抽取中恰有2次抽到使用过零件的概率;
(Ⅱ)从盒中任意抽取3个零件,使用后放回盒子中,设X为盒子中使用过零件的个数,求X的分布列和期望.
(本小题满分13分)已知函数 .
.
(Ⅰ)若 ,求
,求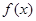 在
在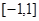 上的最小值;
上的最小值;
(Ⅱ)若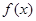 在区间
在区间 上的最大值大于零,求a的取值范围.
上的最大值大于零,求a的取值范围.
(本小题满分13分)在一次射击游戏中,规定每人最多射击3次;在A处击中目标得3分,在B,C处击中目标均得2分,没击中目标不得分;某同学在A处击中目标的概率为 ,在B,C处击中目标的概率均为
,在B,C处击中目标的概率均为 .
.
该同学依次在A,B,C处各射击一次,各次射击之间没有影响,求在一次游戏中:
(Ⅰ)该同学得4分的概率;
(Ⅱ)该同学得分少于5分的概率.
(本小题满分13分)
已知数列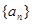 中,
中,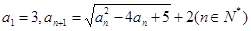 .
.
(Ⅰ)计算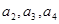 的值;
的值;
(Ⅱ)根据计算结果猜想{an}的通项公式,并用数学归纳法加以证明.
(本大题满分10分)选修4-5:不等式选讲
设函数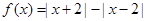
(Ⅰ)解不等式 ;
;
(Ⅱ)当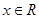 ,
, 时,证明:
时,证明: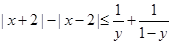 .
.