(本小题满分13分)在一次射击游戏中,规定每人最多射击3次;在A处击中目标得3分,在B,C处击中目标均得2分,没击中目标不得分;某同学在A处击中目标的概率为 ,在B,C处击中目标的概率均为
,在B,C处击中目标的概率均为 .
.
该同学依次在A,B,C处各射击一次,各次射击之间没有影响,求在一次游戏中:
(Ⅰ)该同学得4分的概率;
(Ⅱ)该同学得分少于5分的概率.
已知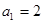 ,点
,点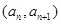
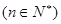 在函数
在函数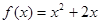 的图象上,设
的图象上,设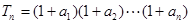 ,
,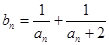 ,数列
,数列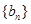 的前
的前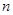 项为
项为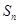 。
。
(1)证明数列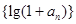 是等比数列;(2)求
是等比数列;(2)求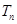 及数列
及数列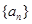 的通项;
的通项;
(3)求证:Sn+ =1
=1
一种填数字彩票2元一张,购买者在 彩票上依次填上0~9中的两个数字(允许重复),中奖规则如下:如果购买者所填的两个数字依次与开奖的四个有序数字分别对应相等,则中一等奖10元;如果购买者所填的两个数字中,只有第二个数字与开奖的第二个数字相等,则中二等奖2元,其他情况均不中奖。
彩票上依次填上0~9中的两个数字(允许重复),中奖规则如下:如果购买者所填的两个数字依次与开奖的四个有序数字分别对应相等,则中一等奖10元;如果购买者所填的两个数字中,只有第二个数字与开奖的第二个数字相等,则中二等奖2元,其他情况均不中奖。
⑴小明和小辉在没有商量的情况下各买了一张这种彩票,求他俩都中一等奖的概率;
⑵求购买一张这种彩票能够中奖的概率;
⑶设购买一张这种彩票的收益为随机变量§,求§的数学期望。
(12分)
已知命题 :
: 是
是 的反函数,且
的反函数,且 ;命题
;命题 :集合
:集合 ,
, ,且
,且 Ф.
Ф.
(Ⅰ)解不等式 (Ⅱ)求使命题
(Ⅱ)求使命题 ,
, 中有且只有一个真命题时实数
中有且只有一个真命题时实数 的取值范围。
的取值范围。
本小题满分12分)
已知向量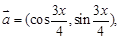

(1)令f(x)= 求f(x)解析式及单调递增区间.
求f(x)解析式及单调递增区间.
(2)若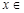
 ,求函数f(x)的最大值和最小值.
,求函数f(x)的最大值和最小值.
已知函数 的定义域是集合
的定义域是集合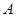 ,函数
,函数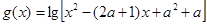 的定义域为集合
的定义域为集合
(Ⅰ)求集合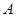 ,
,
(Ⅱ)若 ,求实数
,求实数 的取值范围
的取值范围