如图,在三棱锥S-ABC中,∠SAB=∠SAC=∠ABC=90°,SA=AB,SB=BC.
(Ⅰ)证明:平面SBC⊥平面SAB;
(Ⅱ)求二面角A-SC-B的平面角的正弦值.
已知各项均为正数的数列 的前
的前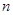 项和为
项和为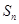 ,且
,且 (
(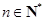 ).
).
(Ⅰ)求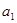 的值及数列
的值及数列 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前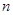 项和为
项和为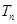 ,求证:
,求证: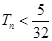 (
(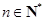 );
);
如图,三棱柱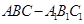 中,
中, ,
, ,平面
,平面 平面
平面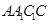 ,
,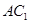 与
与 相交于点
相交于点 .
.
(Ⅰ)求证: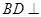 平面
平面 ;
;
(Ⅱ)求二面角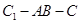 的余弦值.
的余弦值.
某中学校本课程共开设了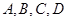 共
共 门选修课,每个学生必须且只能选修
门选修课,每个学生必须且只能选修 门选修课,现有该校的甲、乙、丙
门选修课,现有该校的甲、乙、丙 名学生.
名学生.
(Ⅰ)求这 名学生选修课所有选法的总数;
名学生选修课所有选法的总数;
(Ⅱ)求恰有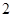 门选修课没有被这
门选修课没有被这 名学生选择的概率;
名学生选择的概率;
(Ⅲ)求 选修课被这
选修课被这 名学生选择的人数
名学生选择的人数 的分布列和数学期望.
的分布列和数学期望.
设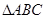 的内角
的内角 所对边的长分别为
所对边的长分别为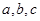 ,且
,且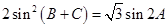 .
.
(Ⅰ)求 的度数;
的度数;
(Ⅱ)若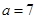 ,
, ,求
,求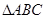 的面积
的面积 .
.
(本小题满分14分)设a为常数,且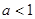 .
.
(1)解关于x的不等式 ;
;
(2)解关于x的不等式组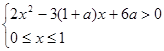 .
.