某企业进行技术改造，有两种方案，甲方案：一次性贷款10万元，第一年便可获利1万元，以后每年比前一年增加30
的利润；乙方案：每年贷款1万元，第一年可获利1万元，以后每年比前一年增加5千元；两次方案的使用期都是10年，到期一次性归还本息。若银行两种形式的贷款都按年息5的复利计算，试比较两种方案中，那种获利更多？
（参考数据1.0510≈1.6 1.310≈13.7 1.510≈55.6）
（本小题满分12分）
从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件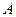
：“取出的2件产品都是二等品”的概率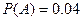
（1）求从该批产品中任取1件是二等品的概率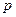
；
（2）若该批产品共10件，从中任意抽取2件，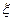
表示取出的2件产品中二等品的件数，求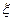的分布列．
（本小题满分12分）
已知函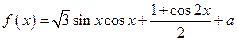数
（
为常数）．
（1）求函数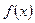
的最小正周期，并指出其单调减区间；
（2）若函数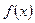在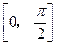
上的最大值是2,试求实数的值.
（本小题满分14分）已知函数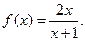
(1)当
时, 证明: 不等式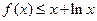
恒成立;
(2)若数列
满足
,证明数列
是等比数列,并求出数列、的通项公式；
(3)在(2)的条件下，若
，证明：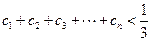
.
(本小题满分14分)已知函数
。
（1）当
时，求曲线
在点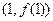
处的切线方程；
（2）求
的单调区间。
(本小题满分14分) 已知中心在坐标原点
的椭圆
经过点
，且点
为其右焦点。
（1）求椭圆的方程；
（2）是否存在平行于
的直线
，使得直线与椭圆有公共点，且直线与的距离等于4？若存在，求出直线的方程；若不存在，请说明理由。