阅读下面的材料，并解答问题：
材料：已知当a、b是正数时，有下列命题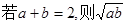
≤1
≤
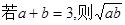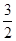
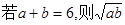≤ 3
（1）根据以上三个命题所提供的规律猜想：
≤ ；
（2）以上规律可用字母表示为 ；
（3）建造一个容积为8立方米，深2米的长方形无盖水池，池底和池壁的造价分别为每平方米120元和80元. 设池底的长为x米，水池总造价为y元，应用上述的规律，求水池的最低造价.
2014年1月，国家发改委出台指导意见，要求2015年底前，所有城市原则上全面实行居民阶梯水价制度．小明为了解市政府调整水价方案的社会反响，随机访问了自己居住在小区的部分居民，就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查，并把调查结果整理成下面的图1，图2．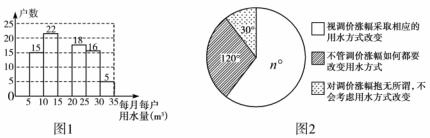
小明发现每月每户的用水量在5m2-35m2之间，有8户居民对用水价格调价涨幅抱无所谓，不用考虑用水方式的改变．根据小明绘制的图表和发现的信息，完成下列问题：
（1）n=，小明调查了户居民，并补全图1；
（2）每月每户用水量的中位数和众数分别落在什么范围？
（3）如果小明所在的小区有1800户居民，请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少？
先化简，再求值：
，其中
，
．
如图，已知一条直线过点
，且与抛物线
交于A，B两点，其中点A的横坐标是
．
（1）求这条直线的函数关系式及点B的坐标；
（2）在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标；若不存在，请说明理由；
（3） 过线段AB上一点P，作PM //x轴，交抛物线于点M，点M在第一象限，点N
，当点M的横坐标为何值时，
的长度最大？最大值是多少？
在数学兴趣小组活动中，小明进行数学探究活动．将边长为2的正方形ABCD与边长为
的正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．
（1）小明发现
，请你帮他说明理由．
（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．
（3）如图3，若小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△
与△
面积之和的最大值，并简要说明理由．
如图，在△ABC中，
，
，D为AC延长线上一点，
．过点D作
//
，交
的延长线于点H．
（1）求
的值；
（2）若
，求AB的长．