2014年1月，国家发改委出台指导意见，要求2015年底前，所有城市原则上全面实行居民阶梯水价制度．小明为了解市政府调整水价方案的社会反响，随机访问了自己居住在小区的部分居民，就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查，并把调查结果整理成下面的图1，图2．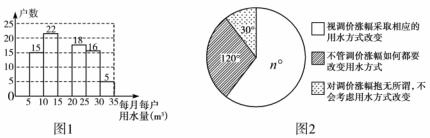
小明发现每月每户的用水量在5m2-35m2之间，有8户居民对用水价格调价涨幅抱无所谓，不用考虑用水方式的改变．根据小明绘制的图表和发现的信息，完成下列问题：
（1）n= ，小明调查了 户居民，并补全图1；
（2）每月每户用水量的中位数和众数分别落在什么范围？
（3）如果小明所在的小区有1800户居民，请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少？
已知：如图，在
中，
的角平分线
交
边于
．
（1）以
边上一点
为圆心，过
两点作
（不写作法，保留作图痕迹），再判断直线与的位置关系，并说明理由；
（2）若（1）中的与边的另一个交点为
，
，求线段
与劣弧
所围成的图形面积．（结果保留根号和
）
如图是某品牌太阳能热火器的实物图和横断面示意图，已知真空集热管
与支架
所在直线相交于水箱横断面
的圆心
，支架与水平面
垂直，
厘米，
，另一根辅助支架
厘米，
．
（1）求垂直支架的长度；（结果保留根号）
（2）求水箱半径
的长度．（结果保留三个有效数字，参考数据：
）
古运河是扬州的母亲河，为打造古运河风光带，现有一段长为180米的河道整治任务由
两工程队先后接力完成．
工作队每天整治12米，
工程队每天整治8米，共用时20天．
（1）根据题意，甲、乙两名同学分别列出尚不完整的方程组如下：
甲：
乙：
根据甲、乙两名同学所列的方程组，请你分别指出未知数
表示的意义，然后在方框中补全甲、乙两名同学所列的方程组：
甲：
表示________________，
表示_______________；
乙：表示________________，表示_______________．
（2）求两工程队分别整治河道多少米．（写出完整的解答过程）
已知：如图，锐角
的两条高
相交于点
，且
（1）求证：是等腰三角形；
（2）判断点是否在
的角平分线上，并说明理由．
扬州市体育中考现场考试内容有三项：50米跑为必测项目；另在立定跳远、实心球（二选一）和坐位体前屈、1分钟跳绳（二选一）中选择两项．
（1）每位考生有__________种选择方案；
（2）用画树状图或列表的方法求小明与小刚选择同种方案的概率．（友情提醒：各种主案用
、…或①、②、③、…等符号来代表可简化解答过程）