如图,已知直角梯形ABCD中,AD∥BC,AB⊥BC ,AD=2cm,AB=8cm,CD=10cm.
(1)求梯形ABCD的周长;
(2)动点P从点B出发,以1cm/s的速度沿B→A→D→C方向向点C运动;动点Q从点C出发,以1cm/s的速度沿C→D→A方向向点A运动;过点Q作QF⊥BC于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之结束,设运动时间为t秒.问:
在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.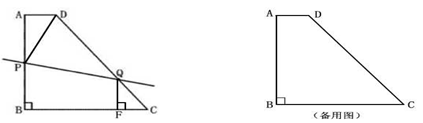
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交点 ,抛物线 过 , 两点,与 轴交于另一点 .
(1)求抛物线的解析式.
(2)在直线 上方的抛物线上有一动点 ,连接 ,与直线 相交于点 ,当 时,求 的值.
(3)点 是抛物线对称轴上一点,在(2)的条件下,若点 位于对称轴左侧,在抛物线上是否存在一点 ,使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点 的坐标;若不存在,请说明理由.

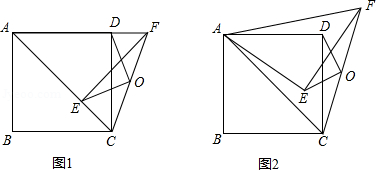
如图,四边形 是正方形,连接 ,将 绕点 逆时针旋转 得 ,连接 , 为 的中点,连接 , .
(1)如图1,当 时,请直接写出 与 的关系(不用证明).
(2)如图2,当 时,(1)中的结论是否成立?请说明理由.
(3)当 时,若 ,请直接写出点 经过的路径长.
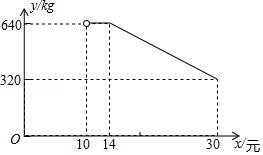
网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克10元.公司在试销售期间,调查发现,每天销售量 与销售单价 (元 满足如图所示的函数关系(其中 .
(1)直接写出 与 之间的函数关系式及自变量的取值范围.
(2)若农贸公司每天销售该特产的利润要达到3100元,则销售单价 应定为多少元?
(3)设每天销售该特产的利润为 元,若 ,求:销售单价 为多少元时,每天的销售利润最大?最大利润是多少元?
如图,四边形 为菱形,以 为直径作 交 于点 ,连接 交 于点 , 是 上的一点,且 ,连接 .
(1)求证: 是 的切线.
(2)若 , ,求 的半径.

小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚 处测得古塔顶端 的仰角为 ,沿山坡向上走 到达 处,测得古塔顶端 的仰角为 .已知山坡坡度 ,即 ,请你帮助小明计算古塔的高度 .(结果精确到 ,参考数据:
