已知 为椭圆
为椭圆
 的左、右焦点,
的左、右焦点, 是坐标原点,过
是坐标原点,过 作垂直于
作垂直于 轴的直线
轴的直线 交椭圆于
交椭圆于
 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过左焦点 的直线
的直线 与椭圆
与椭圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.
(文)袋中有同样的球 个,其中
个,其中 个红色,
个红色, 个黄色,现从中随机地摸
个黄色,现从中随机地摸 球,求:
球,求:
(1)红色球与黄色球恰好相等的概率(用分数表示结果)
(2)红色球多于黄色球的不同摸法的和数.
(理)袋中有同样的球 个,其中
个,其中 个红色,
个红色, 个黄色,现从中随机且不返回地摸球,每次摸
个黄色,现从中随机且不返回地摸球,每次摸 个,当两种颜色的球都被摸到时,即停止摸球,记随机变量
个,当两种颜色的球都被摸到时,即停止摸球,记随机变量 为此时已摸球的次数,求:.
为此时已摸球的次数,求:.
(1)随机变量 的概率分布律;
的概率分布律;
(2)随机变量 的数学期望与方差.
的数学期望与方差.
解关于x、y的二元一次方程组 ,并对解的情况进行讨论.
,并对解的情况进行讨论.
(本小题12分)
已知函数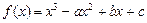 ,
, ,若函数
,若函数 在
在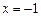 和
和 时取得极值
时取得极值
⑴求实数 ,
, 的值;
的值;
⑵若存在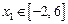 ,
, ,使
,使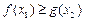 成立,求实数
成立,求实数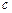 的取值范围.
的取值范围.
(本小题13分)
如图,四棱锥 的底面为正方形,
的底面为正方形, 平面
平面 ,且
,且 ,
, ,
, ,
, 分别是线段
分别是线段 ,
, 的中点.
的中点.
⑴求直线 和
和 所成角的余弦值;
所成角的余弦值;
⑵求二面角 平面角的余弦值.
平面角的余弦值.