某校举办艺术节，其中A班和B班的节目总成绩并列第一，学校决定从A、B两班中选派一个班代表学校参加全省比赛，B班班长想法是：用一个装有质地、大小形状完全相同的8
个红球和6个白球（为正整数）的袋子。由A班班长从中随机摸出一个小球，若摸到的是白球，则选A班去；若摸到的是红球则选B班去。这个办法公平吗？请用概率的知识解释原因
若从袋子中拿出2个红球，再用上述方法确定那个班去，请问对A班还是B班有利？说明理由．
已知关于
的一元二次方程2-
-2=0。
（1）若
=-1是方程的一个根，求的值和方程的另一根；
（2）对于任意实数，判断方程的根的情况，并说明理由。
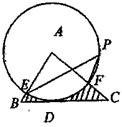
如图，在△ABC中，BC＝4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于E，交AC于F，点P是⊙A上的一点，且∠EPF＝40°，则图中阴影部分的面积是。（结果保留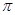
）
如图所示的网格图中，每小格都是边长为1的正方形，△ABC的三个顶点都在格点上，在建立直角坐标系后，点C的坐标（-1，2）。
（1）画出△ABC绕点D（0，5）逆时针旋转90°后的△A1B1C1；并标出△A1B1C1相应各点的坐标。
（2）求点A旋转到A1所经过的路线长。（结果保留π）
已知抛物线的顶点坐标是（8，9），且过点
，求该抛物线的解析式。
解方程（2x－3）2=x2