如图1,将正方形纸片 折叠,使点
折叠,使点 落在
落在 边上一点
边上一点 (不与点
(不与点 ,
, 重合),压平后得到折痕
重合),压平后得到折痕 .
.
当
 时,求
时,求 的值.(方法指导:为了求得
的值.(方法指导:为了求得 的值,可先求
的值,可先求 、
、 的长,不妨设
的长,不妨设 =2)
=2)在图1中,若
 则
则 的值等于 ;若
的值等于 ;若 则
则 的值等于 ;若
的值等于 ;若 (
( 为整数),则
为整数),则 的值等于 .(用含
的值等于 .(用含 的式子表示)
的式子表示)如图2,将矩形纸片
 折叠,使点
折叠,使点 落在
落在 边上一点
边上一点 (不与点
(不与点 重合),压平后得到折痕
重合),压平后得到折痕 设
设 则
则 的值等于 .(用含
的值等于 .(用含 的式子表示)
的式子表示)
先化简,再求值: 2(3x2-y)-(2x2-y),其中x=-2,y=-3
化简
(1)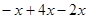
(2)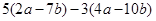
某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式图
(1)第20天的总用水量为多少米3?
(2)求y与x之间的函数关系式;
(3)种植时间为多少天时,总用水量达到7000米3?
如图,在△ABC中,∠B=63°,∠C=51°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数。
如图所示的平面直角坐标系中,三角形ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5)
(1)求三角形ABC的面积
(2)如果将三角形ABC向上平移3个单位长度,得三角形 ,再向右平移2个单位长度,得到三角形
,再向右平移2个单位长度,得到三角形 ,分别画出三角形
,分别画出三角形 和三角形
和三角形 ,并求出
,并求出 的坐标。
的坐标。