如图所示的平面直角坐标系中，三角形ABC的顶点坐标分别是A（0，0）,B（6，0）,C（5，5）
（1）求三角形ABC的面积
（2）如果将三角形ABC向上平移3个单位长度，得三角形
,再向右平移2个单位长度，得到三角形
，分别画出三角形和三角形，并求出
的坐标。
某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染．请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过700台？
解方程：
（1）x2﹣2x﹣8=0；
（2）x（x﹣2）+x﹣2=0．
（本小题满分10分） 如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF、BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC．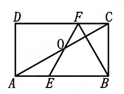
（1）求证：OE=OF；
（2）若BC=2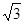
，求AB的长．
（本小题满分10分）如图，一次函数y1=
+1的图象与反比例函数
（k为常数，且k≠0）的图象都经过点A（m，2）．
（1）求点A的坐标及反比例函数的表达式；
（2）结合图象直接比较：当＞0时，
与
的大小．
（本小题满分8分）新华商场销售某种空调，每台进货价为2500元．市场调研表明：当销售价为2900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台．商场要想使这种空调的销售利润平均每天达到5000元，每台空调的定价应为多少元？