(本小题满分10分) 如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.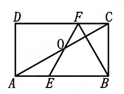
(1)求证:OE=OF;
(2)若BC=2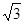 ,求AB的长.
,求AB的长.
如图,已知BD平分∠ABF,且交AE于点D,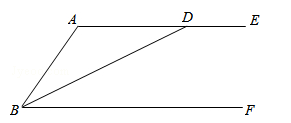
(1)求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);
(2)设AP交BD于点O,交BF于点C,连接CD,当AC⊥BD时,求证:四边形ABCD是菱形.
某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了以下两幅不完整的统计图: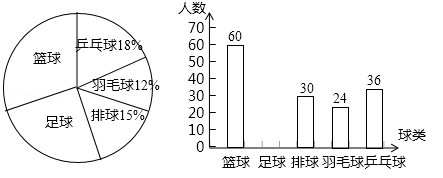
请根据以上统计图提供的信息,解答下列问题:
(1)共抽取_____名学生进行问卷调查;
(2)补全条形统计图,求出扇形统计图中“篮球”所对应的圆心角的度数;
(3)该校共有2500名学生,请估计全校学生喜欢足球运动的人数.
解不等式组: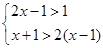 .
.
解方程: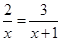 .
.
如图,在平面直角坐标系中,抛物线 经过A(﹣1,0),B(3,0),C(0,3)三点,其顶点为D.连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
经过A(﹣1,0),B(3,0),C(0,3)三点,其顶点为D.连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.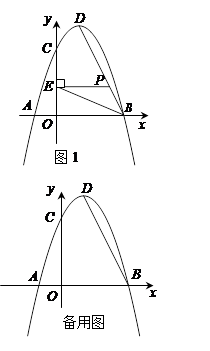
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PBE的面积为S,求S与x的函数关系式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为P′,请求出点P′的坐标.