今年春北方严重干旱,某社区人畜饮水紧张,每天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨,从两水厂运水到社区供水点的路程和运费如下表:
| |
到社区供水点的路程(千米) |
运费(元/吨·千米) |
| 甲厂 |
20 |
12 |
| 乙厂 |
14 |
15 |
若某天调运水的总运费为26700元,则从甲、乙两水厂各调运多少吨饮用水?
设从甲厂调运饮用水
 吨,总运费为W元,试写出W关于与
吨,总运费为W元,试写出W关于与 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?
如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.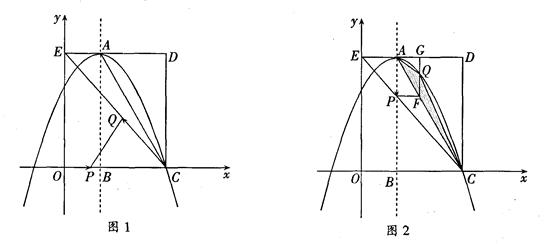
(1)填空:点A坐标为,抛物线的解析式为;
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.连接PQ,是否存在实数t,使得PQ所在的直线经过点D,若存在,求出t的值;若不存在,请说明理由;
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D.
(1)如图1,连接BD并延长BD交AC于点E,连接AD.
①证明:△CDE∽△CAD;
②若AB=2,AC=2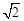 .求CD和CE的长;
.求CD和CE的长;
(2)如图2,过点C作⊙O的另一条切线,切点为F,连结AF、BF,若OC= BF,求
BF,求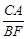 的值.
的值.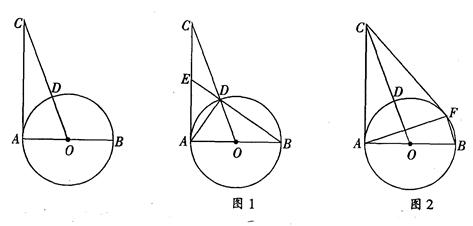
如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形AB-CD的边AB上的“强相似点”,解决问题: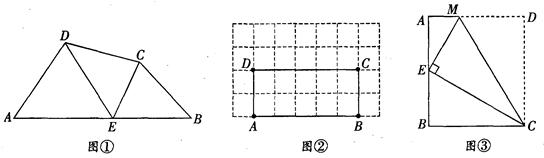
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由:
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
如图,已知二次函数y=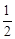 x2-2x+3的图象的顶点为A,且与y轴交于点C.
x2-2x+3的图象的顶点为A,且与y轴交于点C.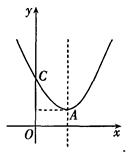
(1)求点A与点C的坐标;
(2)若将此函数的图象沿z轴向右平移1个单位,再沿y轴向下平移3个单位,请直接写出平移后图象所对应的函数关系式及点C的对应点的坐标;
(3)若A(m,y1),B(m+1,y2)两点都在此函数的图象上,试比较y1与y2的大小.
某商场以每件280元的价格购进一批商品,当每件商品的售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.设每件商品的实际售价比原销售价降低了x元.
(1)填表:
(2)要使商场每月销售该商品的利润达到7200元,且更有利于减少库存,则该商品每件实际售价应定为多少元?