设椭圆  :
: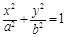 (
(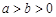 )的一个顶点为
)的一个顶点为 ,
,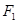 ,
, 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率  ,过椭圆右焦点
,过椭圆右焦点  的直线
的直线  与椭圆
与椭圆 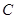 交于
交于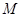 ,
, 两点.
两点.
(1)求椭圆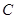 的方程;
的方程;
(2)是否存在直线  ,使得
,使得 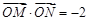 ,若存在,求出直线
,若存在,求出直线  的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
数列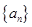 ,
,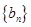 满足
满足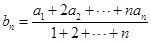
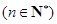 .
.
(1)若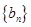 是等差数列,求证:
是等差数列,求证: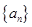 为等差数列;
为等差数列;
(2)若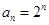 ,求数列
,求数列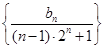 的前
的前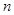 项和
项和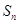 .
.
已知长方体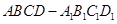 ,点
,点 为
为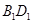 的中点.
的中点.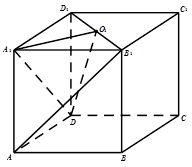
(1)求证: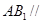 面
面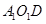 ;
;
(2)若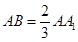 ,试问在线段
,试问在线段 上是否存在点
上是否存在点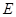 使得
使得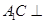
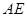 ,若存在求出
,若存在求出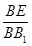 ,若不存在,说明理由.
,若不存在,说明理由.
对某电子元件进行寿命追踪调查,所得情况如下频率分布直方图.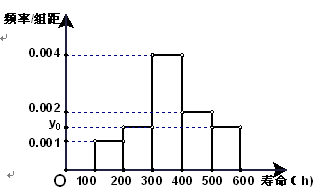
(1)图中纵坐标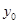 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原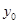 ;
;
(2)根据图表的数据按分层抽样,抽取 个元件,寿命为
个元件,寿命为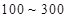 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在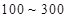 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为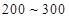 ”的概率.
”的概率.
在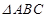 中,角
中,角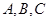 所对的边为
所对的边为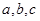 ,角
,角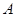 为锐角,若
为锐角,若 ,
, 且
且 .
.
(1)求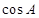 的大小;
的大小;
(2)若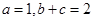 ,求
,求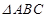 的面积
的面积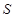 .
.
已知函数 .
.
(Ⅰ)若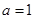 ,求
,求 在点
在点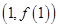 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的极值点;
的极值点;
(Ⅲ)若 恒成立,求
恒成立,求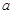 的取值范围.
的取值范围.