已知a,b,c分别为ΔABC三个内角A,B,C的对边长,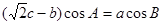 .
.
(Ⅰ)求角A的大小;
(II)若a=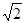 ,ΔABC的面积为1,求b,c.
,ΔABC的面积为1,求b,c.
已知函数f(x)=|x-2|+2|x-a|(a∈R).
(I)当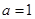 时,解不等式f(x)>3;
时,解不等式f(x)>3;
(II)不等式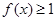 在区间(-∞,+∞)上恒成立,求实数a的取值范围.
在区间(-∞,+∞)上恒成立,求实数a的取值范围.
在平面直角坐标系.x0y中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线 C的极坐标方程为:  .
.
(I)求曲线 的直角坐标方程;
的直角坐标方程;
(II)若直线 的参数方程为
的参数方程为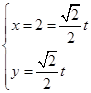 (t为参数),直线
(t为参数),直线 与曲线C相交于A、B两点,求|AB|的值.
与曲线C相交于A、B两点,求|AB|的值.
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A,B,C,D弦AD和BC交于Q点,割线PEF经过Q点交圆O于点E、F,点M在EF上,且 :
:
(I)求证:PA·PB=PM·PQ.
(II)求证: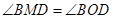 .
.
设函数F(x )=x2+aln(x+1)
(I)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a的取值范围;
(II)若函数y=f(x)有两个极值点x1,x2且 ,求证:
,求证: .
.