已知递增等差数列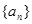 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列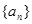 的通项公式
的通项公式 ;
;
(2)若不等式 对任意
对任意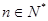 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
如图,已知抛物线
,过点
任作一直线与
相交于
两点,过点
作
轴的平行线与直线
相交于点
(
为坐标原点).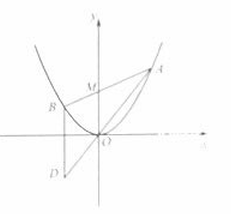
(1)证明:动点
在定直线上;
(2)作
的任意一条切线
(不含
轴)与直线
相交于点
,与(1)中的定直线相交于点
,证明:
为定值,并求此定值.
如图,三棱柱
中,
,
(1)求证:
;
(2)若
,问
为何值时,三棱柱
体积最大,并求此最大值.
已知函数
,其中
.
(1)当
时,求
的单调递增区间;
(2)若
在区间
上的最小值为8,求
的值.
已知数列 的前 项和
(1)求数列
的通项公式;
(2)证明:对任意
,都有
,使得
成等比数列.
已知函数
为奇函数,且
,其中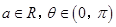
(1)求
的值;
(2)若
,求
的值.